Brutus force attack

It is a kind of attack in which we try to guess the username as well as password. And thus for accomplishing this task we make use of every possible combination of alphabets, numbers (A brute force attack) and words present in dictionary (A dictionary Attack) and as a result those passwords and words which are in dictionary can be guessed and for this Brutus can be used which I’ll use in video to crack the FTP server.

What is brute force and dictionary Attack:-

It is a kind of attack in which we try to guess the username as well as password. And thus for accomplishing this task we make use of every possible combination of alphabets, numbers (A brute force attack) and words present in dictionary (A dictionary Attack) and as a result those passwords and words which are in dictionary can be guessed and for this Brutus can be used which I’ll use in video to crack the FTP server. Similarly there are many other similar softwares. You can download Brutus from here. Rest information is in the video and I’ll tell you
- See more at: http://www.hackersthirst.com/2011/07/dictionary-attack-using-brutus-over-ftp.html#sthash.fdL1oZuh.dpuf

What is brute force and dictionary Attack:-

It is a kind of attack in which we try to guess the username as well as password. And thus for accomplishing this task we make use of every possible combination of alphabets, numbers (A brute force attack) and words present in dictionary (A dictionary Attack) and as a result those passwords and words which are in dictionary can be guessed and for this Brutus can be used which I’ll use in video to crack the FTP server. Similarly there are many other similar softwares. You can download Brutus from here. Rest information is in the video and I’ll tell you
- See more at: http://www.hackersthirst.com/2011/07/dictionary-attack-using-brutus-over-ftp.html#sthash.fdL1oZuh.dpuf

What is Cookie Hijacking

What is Cookie Hijacking.?

Cookie hijacking is also called session hijacking or cookie theft.
Cookie hijacking is a hacking process by which the hacker gains unauthorized access to some confidential information in a way which is not facilitated by the user or a secure session.

Specifically speaking cookie hijacking means hacking or stealing the cookies that contain confidential information that is needed to authenticate or connect a user to a remote web server.

Cookie hijacking can be performed by the hacker by using a computer between the node and server or by obtaining access to the cookies stored on the user’s computer.

A hacker can also use source router Internet protocol or IP packets to gain unauthorized access between two communicating nodes.

The hacker would then route the packets containing cookies to pass through his computer before reaching destination.
Cookie hijacking sometimes is used to perform denial of service attacks also known as DDoS attacks.

Cookie Stealing Attack:

ookie Stealing Attack:

Using this method you can hack Any Account like Facebook ,Twitter , Gmail ,Hotmail ,Skype and yahoo etc.

this works At
LAN(local Area Network) . its best place to hack at university, cafe , public place where computer
are on one LAN simple Example WI-Fi.

What is Cookies And how the use of stealing
cookies?

Cookies are file’s that stored on Any computer’s By any website when a you visits them . the
cookie used by the web server to check the
authenticate the Real user . like you Enter Login in Facebook then a unique string’s Generated and the one copy saved in the web server and other is saved on your Browser as a Cookie file .
both are matched when you open a Account.
so then finally we will start.

Step 1:
Download the Wire Shark and install it.

Step 2:
Next open the wire shark and then click on
interface.

Step 3:
Next choose a interface which is received and
sending packet and click on start

Step 4:
Continue the sniffing for around like 10 minutes.

Step 5:
After a maximum 10 minute stop the sniffing by going to a capture menu.

Step6:
its important step, now filter to http. cookie contains “datr”. Then
filter the all search for http cookies with a name of datr and there is Facebook authentication’s cookie.

Step 7:
Now click on it and then goto the copy > Bytes
> Printable Text only

Step 8:
Now for next step you must have 3 thing,
1. Mozilla Firefox [browser]
2. Grease Monkey[add-on]
3. Cookie injector[code]
and then open facebook. com make sure you are
not login

Step 9:
Press the button Alt C to bring up a cookie
injector and then Simply paste in a cookie value
into it.

Step 10
Now refresh your page so then finally you Enter
the Victim Account.

Note: Only for educational purpose.

Explain how rules are used to facilitate communication.

                                   Figure: commmunication process

Communication :

One definition of communication is “any act by which one person gives to or receives from another person information about that person's needs, desires, perceptions, knowledge, or affective states. Communication may be intentional or unintentional, may involve conventional or unconventional signals, may take linguistic or non-linguistic forms, and may occur through spoken or other modes.
Communication requires a sender, a message, and a recipient, although the receiver doesn't have to be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast distances in time and space. Communication requires that the communicating parties share an area of communicative commonality. The communication process is complete once the receiver understands the sender's message

Establishing the Rules

    An identified sender and receiver
    Agreed upon method of communicating (face-to-face, telephone, letter, photograph)
    Common language and grammar
    Speed and timing of delivery
    Confirmation or acknowledgement requirements

Message Formatting and Encapsulation

CCNA SOLUTIONS

CHAPTER 1

1.     Explain how multiple networks are used in everyday life.
2.     Explain the topologies and devices used in a small to medium-sized business network.
3.     Explain the basic characteristics of a network
4.     Explain trends in networking that will affect the use of networks in small to medium-sized businesses

CHAPTER 2

1.     Explain the purpose of Cisco IOS.
2.     Explain how to access and navigate Cisco IOS to configure network devices.
3.     Describe the command structure of Cisco IOS software.
4.     Configure hostnames on a Cisco IOS device using the CLI.
5.     Use Cisco IOS commands to limit access to device configurations.
6.     Use Cisco IOS commands to save the running configuration.
7.     Explain how devices communicate across network media.
8.     Configure a host device with an IP address.
9.     Verify connectivity between two end devices.

CHAPTER 3

1.     Explain how rules are used to facilitate communication.
2.     Explain the role of protocols and standards organizations in facilitating interoperability in network communications.
3.     Explain how devices on a LAN access resources in a small to medium-sized business network.

Chapter 4

1.     Explain how physical layer protocols and services support communications across data networks.
2.     Build a simple network using the appropriate.
3.     Explain the role of the data link layer in supporting communications across data networks.
4.     Compare media access control techniques and logical topologies used in networks.

CHAPTER 5
 

1.     Describe the operation of the Ethernet sublayers.
2.     Identify the major fields of the Ethernet frame.
3.     Describe the purpose and characteristics of the Ethernet MAC address.
4.     Describe the purpose of ARP.
5.     Explain how ARP requests impact network and host performance.
6.     Explain basic switching concepts.
7.     Compare fixed configuration and modular switches.
8.     Configure a Layer 3 switch.

CONCLUSION.

6. CONCLUSION... OF SORTS

This paper has briefly described how cryptography works. The reader must beware, however, that there are a number of ways to attack every one of these systems; cryptanalysis and attacks on cryptosystems, however, are well beyond the scope of this paper. In the words of Sherlock Holmes (ok, Arthur Conan Doyle, really), "What one man can invent, another can discover" ("The Adventure of the Dancing Men").
Cryptography is a particularly interesting field because of the amount of work that is, by necessity, done in secret. The irony is that secrecy is not the key to the goodness of a cryptographic algorithm. Regardless of the mathematical theory behind an algorithm, the best algorithms are those that are well-known and well-documented because they are also well-tested and well-studied! In fact, time is the only true test of good cryptography; any cryptographic scheme that stays in use year after year is most likely a good one. The strength of cryptography lies in the choice (and management) of the keys; longer keys will resist attack better than shorter keys.
The corollary to this is that consumers should run, not walk, away from any product that uses a proprietary cryptography scheme, ostensibly because the algorithm's secrecy is an advantage. The observation that a cryptosystem should be secure even if everything about the system — except the key — is known by your adversary has been a fundamental tenet of cryptography for over 125 years. It was first stated by Dutch linguist Auguste Kerckhoffs von Nieuwenhoff in his 1883 (yes, 1883) papers titled La Cryptographie militaire, and has therefore become known as "Kerckhoffs' Principle."

Getting a new crypto methodology accepted and, therefore, commercially viable, is always an interesting challenge. And speaking of challenges, take a look at the DioCipher $10,000 challenge page (expires 1 January 2013). I leave it to the reader to consider the validity and usefulness of the process, the challenge, and — ultimately — the algorithm!

CRYPTOGRAPHIC ALGORITHMS IN ACTION

5.

CRYPTOGRAPHIC ALGORITHMS IN ACTION

The paragraphs above have provided an overview of the different types of cryptographic algorithms, as well as some examples of some available protocols and schemes. Table 3 provides a list of some other noteworthy schemes employed — or proposed — for a variety of functions, most notably electronic commerce. The paragraphs below will show several real cryptographic applications that many of us employ (knowingly or not) everyday for password protection and private communication.

TABLE 3. Other Crypto Algorithms and Systems of Note.

Capstone	A now-defunct U.S. National Institute of Standards and Technology (NIST) and National Security Agency (NSA) project under the Bush Sr. and Clinton administrations for publicly available strong cryptography with keys escrowed by the government (NIST and the Treasury Dept.). Capstone included in one or more tamper-proof computer chips for implementation (Clipper), a secret key encryption algorithm (Skipjack), digital signature algorithm (DSA), key exchange algorithm (KEA), and hash algorithm (SHA).
Clipper	The computer chip that would implement the Skipjack encryption scheme. See also EPIC's The Clipper Chip Web page.
Escrowed Encryption Standard (EES)	Largely unused, a controversial crypto scheme employing the SKIPJACK secret key crypto algorithm and a Law Enforcement Access Field (LEAF) creation method. LEAF was one part of the key escrow system and allowed for decryption of ciphertext messages that had been legally intercepted by law enforcement agencies. Described more in FIPS 185.
Federal Information Processing Standards (FIPS)	These computer security- and crypto-related FIPS are produced by the U.S. National Institute of Standards and Technology (NIST) as standards for the U.S. Government.
Fortezza (formerly called Tessera)	A PCMCIA card developed by NSA that implements the Capstone algorithms, intended for use with the Defense Messaging Service (DMS).
GOST	GOST is a family of algorithms that is defined in the Russian cryptographic standards. Although most of the specifications are written in Russian, a series of RFCs describe some of the aspects so that the algorithms can be used effectively in Internet applications: RFC 4357: Additional Cryptographic Algorithms for Use with GOST 28147-89, GOST R 34.10-94, GOST R 34.10-2001, and GOST R 34.11-94 Algorithms RFC 5830: GOST 28147-89: Encryption, Decryption, and Message Authentication Code (MAC) Algorithms RFC 6986: GOST R 34.11-2012: Hash Function Algorithm RFC 7091: GOST R 34.10-2012: Digital Signature Algorithm (Updates RFC 5832: GOST R 34.10-2001)
Identity-Based Encryption (IBE)	Identity-Based Encryption was first proposed by Adi Shamir in 1984, and is a key authentication system where the public key can be derived from some unique information based upon the user's identity. In 2001, Dan Boneh (Stanford) and Matt Franklin (U.C., Davis) developed a practical implementation of IBE based on elliptic curves and a mathematical construct called the Weil Pairing. In that year, Clifford Cocks (GCHQ) also described another IBE solution based on quadratic residues in composite groups. RFC 5091: Identity-Based Cryptography Standard (IBCS) #1: Describes an implementation of IBE using Boneh-Franklin (BF) and Boneh-Boyen (BB1) Identity-based Encryption. This document is in part based on Voltage Security's Identity-based Cryptography Standards (IBCS) documents.
IP Security Protocol (IPsec)	The IPsec protocol suite is used to provide privacy and authentication services at the IP layer. An overview of the protocol suite and of the documents comprising IPsec can be found in RFC 2411. Other documents include: RFC 4301: IP security architecture. RFC 4302: IP Authentication Header (AH), one of the two primary IPsec functions; AH provides connectionless integrity and data origin authentication for IP datagrams and protects against replay attacks. RFC 4303: IP Encapsulating Security Payload (ESP), the other primary IPsec function; ESP provides a variety of security services within IPsec. RFC 4304: Extended Sequence Number (ESN) Addendum, allows for negotiation of a 32- or 64- bit sequence number, used to detect replay attacks. RFC 4305: Cryptographic algorithm implementation requirements for ESP and AH. RFC 5996: The Internet Key Exchange (IKE) protocol, version 2, providing for mutual authentication and establishing and maintaining security associations. IKE v1 was described in three separate documents, RFC 2407 (application of ISAKMP to IPsec), RFC 2408 (ISAKMP, a framework for key management and security associations), and RFC 2409 (IKE, using part of Oakley and part of SKEME in conjunction with ISAKMP to obtain authenticated keying material for use with ISAKMP, and for other security associations such as AH and ESP). IKE v1 is obsoleted with the introdcution of IKEv2. RFC 4307: Cryptographic algoritms used with IKEv2. RFC 4308: Crypto suites for IPsec, IKE, and IKEv2. RFC 4309: The use of AES in CBC-MAC mode with IPsec ESP. RFC 4312: The use of the Camellia cipher algorithm in IPsec. RFC 4359: The Use of RSA/SHA-1 Signatures within Encapsulating Security Payload (ESP) and Authentication Header (AH). RFC 4434: Describes AES-XCBC-PRF-128, a pseudo-random function derived from the AES for use with IKE. RFC 2403: Describes use of the HMAC with MD5 algorithm for data origin authentication and integrity protection in both AH and ESP. RFC 2405: Describes use of DES-CBC (DES in Cipher Block Chaining Mode) for confidentiality in ESP. RFC 2410: Defines use of the NULL encryption algorithm (i.e., provides authentication and integrity without confidentiality) in ESP. RFC 2412: Describes OAKLEY, a key determination and distribution protocol. RFC 2451: Describes use of Cipher Block Chaining (CBC) mode cipher algorithms with ESP. RFCs 2522 and 2523: Description of Photuris, a session-key management protocol for IPsec. In addition, RFC 6379 describes Suite B Cryptographic Suites for IPsec and RFC 6380 describes the Suite B profile for IPsec. IPsec was first proposed for use with IP version 6 (IPv6), but can also be employed with the current IP version, IPv4. (See more detail about IPsec below in Section 5.6.)
Internet Security Association and Key Management Protocol (ISAKMP/OAKLEY)	ISAKMP/OAKLEY provide an infrastructure for Internet secure communications. ISAKMP, designed by the National Security Agency (NSA) and described in RFC 2408, is a framework for key management and security associations, independent of the key generation and cryptographic algorithms actually employed. The OAKLEY Key Determination Protocol, described in RFC 2412, is a key determination and distribution protocol using a variation of Diffie-Hellman.
Kerberos	A secret-key encryption and authentication system, designed to authenticate requests for network resources within a user domain rather than to authenticate messages. Kerberos also uses a trusted third-party approach; a client communications with the Kerberos server to obtain "credentials" so that it may access services at the application server. Kerberos V4 uses DES to generate keys and encrypt messages; DES is also commonly used in Kerberos V5, although other schemes could be employed. Microsoft added support for Kerberos V5 — with some proprietary extensions — in Windows 2000. There are many Kerberos articles posted at Microsoft's Knowledge Base, notably "Basic Overview of Kerberos User Authentication Protocol in Windows 2000," "Windows 2000 Kerberos 5 Ticket Flags and KDC Options for AS_REQ and TGS_REQ Messages," and "Kerberos Administration in Windows 2000."
Keyed-Hash Message Authentication Code (HMAC)	A message authentication scheme based upon secret key cryptography and the secret key shared between two parties rather than public key methods. Described in FIPS 198 and RFC 2104.
Message Digest Cipher (MDC)	Invented by Peter Gutman, MDC turns a one-way hash function into a block cipher.
MIME Object Security Standard (MOSS)	Designed as a successor to PEM to provide PEM-based security services to MIME messages.
NSA Suite B Cryptography	An NSA standard for securing information at the SECRET level. Defines use of: Advanced Encryption Standard (AES) with key sizes of 128 and 256 bits, per FIPS PUB 197 for encryption The Ephemeral Unified Model and the One-Pass Diffie Hellman (referred to as ECDH) using the curves with 256 and 384-bit prime moduli, per NIST Special Publication 800-56A for key exchange Elliptic Curve Digital Signature Algorithm (ECDSA) using the curves with 256 and 384-bit prime moduli, per FIPS PUB 186-3 for digital signatures Secure Hash Algorithm (SHA) using 256 and 384 bits, per FIPS PUB 180-3 for hashing RFC 6239 describes Suite B Cryptographic Suites for Secure Shell (SSH) and RFC 6379 describes Suite B Cryptographic Suites for Secure IP (IPsec).
Pretty Good Privacy (PGP)	A family of cryptographic routines for e-mail and file storage applications developed by Philip Zimmermann. PGP 2.6.x uses RSA for key management and digital signatures, IDEA for message encryption, and MD5 for computing the message's hash value; more information can also be found in RFC 1991. PGP 5.x (formerly known as "PGP 3") uses Diffie-Hellman/DSS for key management and digital signatures; IDEA, CAST, or 3DES for message encryption; and MD5 or SHA for computing the message's hash value. OpenPGP, described in RFC 2440, is an open definition of security software based on PGP 5.x. (See more detail about PGP below in Section 5.5.)
Privacy Enhanced Mail (PEM)	Provides secure electronic mail over the Internet and includes provisions for encryption (DES), authentication, and key management (DES, RSA). May be superseded by S/MIME and PEM-MIME. Developed by IETF PEM Working Group and defined in four RFCs: RFC 1421: Part I, Message Encryption and Authentication Procedures RFC 1422: Part II, Certificate-Based Key Management RFC 1423: Part III, Algorithms, Modes, and Identifiers RFC 1424: Part IV, Key Certification and Related Services
Private Communication Technology (PCT)	Developed by Microsoft and Visa for secure communication on the Internet. Similar to SSL, PCT supports Diffie-Hellman, Fortezza, and RSA for key establishment; DES, RC2, RC4, and triple-DES for encryption; and DSA and RSA message signatures. A companion to SET.
Secure Electronic Transactions (SET)	A merging of two other protocols: SEPP (Secure Electronic Payment Protocol), an open specification for secure bank card transactions over the Internet, developed by CyberCash, GTE, IBM, MasterCard, and Netscape; and STT (Secure Transaction Technology), a secure payment protocol developed by Microsoft and Visa International. Supports DES and RC4 for encryption, and RSA for signatures, key exchange, and public-key encryption of bank card numbers. SET is a companion to the PCT protocol.
Secure Hypertext Transfer Protocol (S-HTTP)	An extension to HTTP to provide secure exchange of documents over the World Wide Web. Supported algorithms include RSA and Kerberos for key exchange, DES, IDEA, RC2, and Triple-DES for encryption.
Secure Multipurpose Internet Mail Extensions (S/MIME)	An IETF secure e-mail scheme intended to supercede PEM. S/MIME, described in RFCs 2311 and 2312, adds digital signature and encryption capability to Internet MIME messages.
Secure Sockets Layer (SSL)	Developed by Netscape Communications to provide application-independent security and privacy over the Internet. SSL is designed so that protocols such as HTTP, FTP (File Transfer Protocol), and Telnet can operate over it transparently. SSL allows both server authentication (mandatory) and client authentication (optional). RSA is used during negotiation to exchange keys and identify the actual cryptographic algorithm (DES, IDEA, RC2, RC4, or 3DES) to use for the session. SSL also uses MD5 for message digests and X.509 public-key certificates. (Found to be breakable soon after the IETF announced formation of group to work on TLS.) SSL version 3.0 is described in RFC 6101. (See more detail about SSL below in Section 5.7.)
Server Gated Cryptography (SGC)	Microsoft extension to SSL that provides strong encryption for online banking and other financial applications using RC2 (128-bit key), RC4 (128-bit key), DES (56-bit key), or 3DES (equivalent of 168-bit key). Use of SGC requires a Windows NT Server running Internet Information Server (IIS) 4.0 with a valid SGC certificate. SGC is available in 32-bit Windows versions of Internet Explorer (IE) 4.0, and support for Mac, Unix, and 16-bit Windows versions of IE is expected in the future.
Simple Authentication and Security Layer (SASL)	(SASL) is a framework for providing authentication and data security services in connection-oriented protocols (a la TCP). It provides a structured interface and allows new protocols to reuse existing authentication mechanisms and allows old protocols to make use of new mechanisms. It has been common practice on the Internet to permit anonymous access to various services, employing a plain-text password using a user name of "anonymous" and a password of an email address or some other identifying information. New IETF protocols disallow plain-text logins. The Anonymous SASL Mechanism (RFC 4505) provides a method for anonymous logins within the SASL framework.
Simple Key-Management for Internet Protocol (SKIP)	Key management scheme for secure IP communication, specifically for IPsec, and designed by Aziz and Diffie. SKIP essentially defines a public key infrastructure for the Internet and even uses X.509 certificates. Most public key cryptosystems assign keys on a per-session basis, which is inconvenient for the Internet since IP is connectionless. Instead, SKIP provides a basis for secure communication between any pair of Internet hosts. SKIP can employ DES, 3DES, IDEA, RC2, RC5, MD5, and SHA-1.
Transport Layer Security (TLS)	TLS v1.0 is an IETF specification (RFC 2246) intended to replace SSL. TLS v1.0 employs Triple-DES (secret key cryptography), SHA (hash), Diffie-Hellman (key exchange), and DSS (digital signatures). TLS v1.0 has been shown to be vulnerable to attack and has been updated by v1.1 (RFC 4346) and v1.2 (RFC 5246. TLS is designed to operate over TCP. The IETF developed the Datagram Transport Layer Security (DTLS) protocol to operate over UDP. DTLS v1.2 is described in RFC 6347. (See more detail about TLS below in Section 5.7.)
TrueCrypt	Open source, multi-platform cryptography software that can be used to encrypt a file, partition, or entire disk. One of TrueCrypt's more interesting features is that of plausible deniability with hidden volumes or hidden operating systems. (See more detail about TrueCrypt below in Section 5.11.)
X.509	ITU-T recommendation for the format of certificates for the public key infrastructure. Certificates map (bind) a user identity to a public key. The IETF application of X.509 certificates is documented in RFC 2459. An Internet X.509 Public Key Infrastructure is further defined in RFC 2510 (Certificate Management Protocols) and RFC 2527 (Certificate Policy and Certification Practices Framework).

5.1. Password Protection

Nearly all modern multiuser computer and network operating systems employ passwords at the very least to protect and authenticate users accessing computer and/or network resources. But passwords are not typically kept on a host or server in plaintext, but are generally encrypted using some sort of hash scheme.

A) /etc/passwd file root:Jbw6BwE4XoUHo:0:0:root:/root:/bin/bash carol:FM5ikbQt1K052:502:100:Carol Monaghan:/home/carol:/bin/bash alex:LqAi7Mdyg/HcQ:503:100:Alex Insley:/home/alex:/bin/bash gary:FkJXupRyFqY4s:501:100:Gary Kessler:/home/gary:/bin/bash todd:edGqQUAaGv7g6:506:101:Todd Pritsky:/home/todd:/bin/bash josh:FiH0ONcjPut1g:505:101:Joshua Kessler:/home/webroot:/bin/bash B.1) /etc/passwd file (with shadow passwords) root:x:0:0:root:/root:/bin/bash carol:x:502:100:Carol Monaghan:/home/carol:/bin/bash alex:x:503:100:Alex Insley:/home/alex:/bin/bash gary:x:501:100:Gary Kessler:/home/gary:/bin/bash todd:x:506:101:Todd Pritsky:/home/todd:/bin/bash josh:x:505:101:Joshua Kessler:/home/webroot:/bin/bash B.2) /etc/shadow file root:AGFw$1$P4u/uhLK$l2.HP35rlu65WlfCzq:11449:0:99999:7::: carol:kjHaN%35a8xMM8a/0kMl1?fwtLAM.K&kw.:11449:0:99999:7::: alex:1$1KKmfTy0a7#3.LL9a8H71lkwn/.hH22a:11449:0:99999:7::: gary:9ajlknknKJHjhnu7298ypnAIJKL$Jh.hnk:11449:0:99999:7::: todd:798POJ90uab6.k$klPqMt%alMlprWqu6$.:11492:0:99999:7::: josh:Awmqpsui*787pjnsnJJK%aappaMpQo07.8:11492:0:99999:7::: FIGURE 5: Sample entries in Unix/Linux password files.

Unix/Linux, for example, uses a well-known hash via its crypt() function. Passwords are stored in the /etc/passwd file (Figure 5A); each record in the file contains the username, hashed password, user's individual and group numbers, user's name, home directory, and shell program; these fields are separated by colons (:). Note that each password is stored as a 13-byte string. The first two characters are actually a salt, randomness added to each password so that if two users have the same password, they will still be encrypted differently; the salt, in fact, provides a means so that a single password might have 4096 different encryptions. The remaining 11 bytes are the password hash, calculated using DES.
As it happens, the /etc/passwd file is world-readable on Unix systems. This fact, coupled with the weak encryption of the passwords, resulted in the development of the shadow password system where passwords are kept in a separate, non-world-readable file used in conjunction with the normal password file. When shadow passwords are used, the password entry in /etc/passwd is replaced with a "*" or "x" (Figure 5B.1) and the MD5 hash of the passwords are stored in /etc/shadow along with some other account information (Figure 5B.2).
Windows NT uses a similar scheme to store passwords in the Security Access Manager (SAM) file. In the NT case, all passwords are hashed using the MD4 algorithm, resulting in a 128-bit (16-byte) hash value (they are then obscured using an undocumented mathematical transformation that was a secret until distributed on the Internet). The password password, for example, might be stored as the hash value (in hexadecimal) 60771b22d73c34bd4a290a79c8b09f18.
Passwords are not saved in plaintext on computer systems precisely so they cannot be easily compromised. For similar reasons, we don't want passwords sent in plaintext across a network. But for remote logon applications, how does a client system identify itself or a user to the server? One mechanism, of course, is to send the password as a hash value and that, indeed, may be done. A weakness of that approach, however, is that an intruder can grab the password off of the network and use an off-line attack (such as a dictionary attack where an attacker takes every known word and encrypts it with the network's encryption algorithm, hoping eventually to find a match with a purloined password hash). In some situations, an attacker only has to copy the hashed password value and use it later on to gain unauthorized entry without ever learning the actual password.
An even stronger authentication method uses the password to modify a shared secret between the client and server, but never allows the password in any form to go across the network. This is the basis for the Challenge Handshake Authentication Protocol (CHAP), the remote logon process used by Windows NT.
As suggested above, Windows NT passwords are stored in a security file on a server as a 16-byte hash value. In truth, Windows NT stores two hashes; a weak hash based upon the old LAN Manager (LanMan) scheme and the newer NT hash. When a user logs on to a server from a remote workstation, the user is identified by the username, sent across the network in plaintext (no worries here; it's not a secret anyway!). The server then generates a 64-bit random number and sends it to the client (also in plaintext). This number is the challenge.
Using the LanMan scheme, the client system then encrypts the challenge using DES. Recall that DES employs a 56-bit key, acts on a 64-bit block of data, and produces a 64-bit output. In this case, the 64-bit data block is the random number. The client actually uses three different DES keys to encrypt the random number, producing three different 64-bit outputs. The first key is the first seven bytes (56 bits) of the password's hash value, the second key is the next seven bytes in the password's hash, and the third key is the remaining two bytes of the password's hash concatenated with five zero-filled bytes. (So, for the example above, the three DES keys would be 60771b22d73c34, bd4a290a79c8b0, and 9f180000000000.) Each key is applied to the random number resulting in three 64-bit outputs, which comprise the response. Thus, the server's 8-byte challenge yields a 24-byte response from the client and this is all that would be seen on the network. The server, for its part, does the same calculation to ensure that the values match.
There is, however, a significant weakness to this system. Specifically, the response is generated in such a way as to effectively reduce 16-byte hash to three smaller hashes, of length seven, seven, and two. Thus, a password cracker has to break at most a 7-byte hash. One Windows NT vulnerability test program that I have used in the past will report passwords that are "too short," defined as "less than 8 characters." When I asked how the program knew that passwords were too short, the software's salespeople suggested to me that the program broke the passwords to determine their length. This is undoubtedly not true; all the software really has to do is look at the second 7-byte block and some known value indicates that it is empty, which would indicate a password of seven or less characters.
Consider the following example, showing the LanMan hash of two different short passwords (take a close look at the last 8 bytes):

AA:	89D42A44E77140AAAAD3B435B51404EE
AAA:	1C3A2B6D939A1021AAD3B435B51404EE

Note that the NT hash provides no such clue:

AA:	C5663434F963BE79C8FD99F535E7AAD8
AAA:	6B6E0FB2ED246885B98586C73B5BFB77

It is worth noting that the discussion above describes the Microsoft version of CHAP, or MS-CHAP (MS-CHAPv2 is described in RFC 2759). MS-CHAP assumes that it is working with hashed values of the password as the key to encrypting the challenge. More traditional CHAP (RFC 1994) assumes that it is starting with passwords in plaintext. The relevance of this observation is that a CHAP client, for example, cannot be authenticated by an MS-CHAP server; both client and server must use the same CHAP version.

5.2. Some of the Finer Details of Diffie-Hellman

Diffie and Hellman introduced the concept of public-key cryptography. The mathematical "trick" of Diffie-Hellman key exchange is that it is relatively easy to compute exponents compared to computing discrete logarithms. Diffie-Hellman allows two parties — the ubiquitous Alice and Bob — to generate a secret key; they need to exchange some information over an unsecure communications channel to perform the calculation but an eavesdropper cannot determine the shared secret key based upon this information.
Diffie-Hellman works like this. Alice and Bob start by agreeing on a large prime number, N. They also have to choose some number G so that G<N.
There is actually another constraint on G, namely that it must be primitive with respect to N. Primitive is a definition that is a little beyond the scope of our discussion but basically G is primitive to N if we can find integers i so that Gⁱ = j mod N for all values of j from 1 to N-1. As an example, 2 is not primitive to 7 because the set of powers of 2 from 1 to 6, mod 7 (i.e., 2¹ mod 7, 2² mod 7 ... 2⁶ mod 7) = {2,4,1,2,4,1}. On the other hand, 3 is primitive to 7 because the set of powers of 3 from 1 to 6, mod 7 = {3,2,6,4,5,1}.
(The definition of primitive introduced a new term to some readers, namely mod. The phrase x mod y (and read as written!) means "take the remainder after dividing x by y." Thus, 1 mod 7 = 1, 9 mod 6 = 3, and 8 mod 8 = 0. Read more about the modulo function in the appendix.)
Anyway, either Alice or Bob selects N and G; they then tell the other party what the values are. Alice and Bob then work independently:

Alice... Choose a large random number, XA < N. This is Alice's private key. Compute YA = GXA mod N. This is Alice's public key. Exchange public key's with Bob. Compute KA = YBXA mod N

Bob... Choose a large random number, XB < N. This is Bob's private key. Compute YB = GXB mod N. This is Bob's public key. Exchange public key's with Alice. Compute KB = YAXB mod N

Note that X_A and X_B are kept secret while Y_A and Y_B are openly shared; these are the private and public keys, respectively. Based on their own private key and the public key learned from the other party, Alice and Bob have computed their secret keys, K_A and K_B, respectively, which are equal to G^X_AX_B mod N.
Perhaps a small example will help here. Although Alice and Bob will really choose large values for N and G, I will use small values for example only; let's use N=7 and G=3.

Alice... Choose XA = 2 Calculate YA = 32 mod 7 = 2 Exchange public keys with Bob KA = 62 mod 7 = 1

Bob... Choose XB = 3 Calculate YB = 33 mod 7 = 6 Exchange public keys with Alice KB = 23 mod 7 = 1

In this example, then, Alice and Bob will both find the secret key 1 which is, indeed, 3⁶ mod 7 (i.e., G^X_AX_B = 3^2˙3). If an eavesdropper (Mallory) was listening in on the information exchange between Alice and Bob, he would learn G, N, Y_A, and Y_B which is a lot of information but insufficient to compromise the key; as long as X_A and X_B remain unknown, K is safe. As said above, calculating Y = G^X is a lot easier than finding X = log_G Y.

A short digression on modulo arithmetic. In the paragraph above, we noted that 3⁶ mod 7 = 1. This can be confirmed, of course, by noting that:

3⁶ = 729 = 104*7 + 1

There is a nice property of modulo arithmetic, however, that makes this determination a little easier, namely: (a mod x)(b mod x) = (ab mod x). Therefore, one possible shortcut is to note that 3⁶ = (3³)(3³). Therefore, 3⁶ mod 7 = (3³ mod 7)(3³ mod 7) = (27 mod 7)(27 mod 7) = 6*6 mod 7 = 36 mod 7 = 1.

Diffie-Hellman can also be used to allow key sharing amongst multiple users. Note again that the Diffie-Hellman algorithm is used to generate secret keys, not to encrypt and decrypt messages.

5.3. Some of the Finer Details of RSA Public-Key Cryptography

Unlike Diffie-Hellman, RSA can be used for key exchange as well as digital signatures and the encryption of small blocks of data. Today, RSA is primarily used to encrypt the session key used for secret key encryption (message integrity) or the message's hash value (digital signature). RSA's mathematical hardness comes from the ease in calculating large numbers and the difficulty in finding the prime factors of those large numbers. Although employed with numbers using hundreds of digits, the math behind RSA is relatively straight-forward.
To create an RSA public/private key pair, here are the basic steps:

1. Choose two prime numbers, p and q. From these numbers you can calculate the modulus, n = pq.
2. Select a third number, e, that is relatively prime to (i.e., it does not divide evenly into) the product (p-1)(q-1). The number e is the public exponent.
3. Calculate an integer d from the quotient (ed-1)/[(p-1)(q-1)]. The number d is the private exponent.

The public key is the number pair (n,e). Although these values are publicly known, it is computationally infeasible to determine d from n and e if p and q are large enough.
To encrypt a message, M, with the public key, create the ciphertext, C, using the equation:

C = M^e mod n

The receiver then decrypts the ciphertext with the private key using the equation:

M = C^d mod n

Now, this might look a bit complex and, indeed, the mathematics does take a lot of computer power given the large size of the numbers; since p and q may be 100 digits (decimal) or more, d and e will be about the same size and n may be over 200 digits. Nevertheless, a simple example may help. In this example, the values for p, q, e, and d are purposely chosen to be very small and the reader will see exactly how badly these values perform, but hopefully the algorithm will be adequately demonstrated:

1. Select p=3 and q=5.
2. The modulus n = pq = 15.
3. The value e must be relatively prime to (p-1)(q-1) = (2)(4) = 8. Select e=11
4. The value d must be chosen so that (ed-1)/[(p-1)(q-1)] is an integer. Thus, the value (11d-1)/[(2)(4)] = (11d-1)/8 must be an integer. Calculate one possible value, d=3.
5. Let's say we wish to send the string SECRET. For this example, we will convert the string to the decimal representation of the ASCII values of the characters, which would be 83 69 67 82 69 84.
6. The sender encrypts each digit one at a time (we have to because the modulus is so small) using the public key value (e,n)=(11,15). Thus, each ciphertext character C_i = M_i¹¹ mod 15. The input digit string 0x836967826984 will be transmitted as 0x2c696d286924.
7. The receiver decrypts each digit using the private key value (d,n)=(3,15). Thus, each plaintext character M_i = C_i³ mod 15. The input digit string 0x2c696d286924 will be converted to 0x836967826984 and, presumably, reassembled as the plaintext string SECRET.

Again, the example above uses small values for simplicity and, in fact, shows the weakness of small values; note that 4, 6, and 9 do not change when encrypted, and that the values 2 and 8 encrypt to 8 and 2, respectively. Nevertheless, this simple example demonstrates how RSA can be used to exchange information.
RSA keylengths of 512 and 768 bits are considered to be pretty weak. The minimum suggested RSA key is 1024 bits; 2048 and 3072 bits are even better.
As an aside, Adam Back (http://www.cypherspace.org/~adam/) wrote a two-line Perl script to implement RSA. It employs dc, an arbitrary precision arithmetic package that ships with most UNIX systems:

print pack"C*",split/\D+/,`echo "16iII*o\U@{$/=$z;[(pop,pop,unpack"H*",<> )]}\EsMsKsN0[lN*1lK[d2%Sa2/d0<X+d*lMLa^*lN%0]dsXx++lMlN/dsM0<J]dsJxp"|dc`

5.4. Some of the Finer Details of DES, Breaking DES, and DES Variants

The Data Encryption Standard (DES) has been in use since the mid-1970s, adopted by the National Bureau of Standards (NBS) [now the National Institute for Standards and Technology (NIST)] as Federal Information Processing Standard 46 (FIPS 46-3) and by the American National Standards Institute (ANSI) as X3.92.
As mentioned earlier, DES uses the Data Encryption Algorithm (DEA), a secret key block-cipher employing a 56-bit key operating on 64-bit blocks. FIPS 81 describes four modes of DES operation: Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB). Despite all of these options, ECB is the most commonly deployed mode of operation.
NIST finally declared DES obsolete in 2004, and withdrew FIPS 46-3, 74, and 81 (Federal Register, July 26, 2004, 69(142), 44509-44510). Although other block ciphers will replace DES, it is still interesting to see how DES encryption is performed; not only is it sort of neat, but DES was the first crypto scheme commonly seen in non-govermental applications and was the catalyst for modern "public" cryptography. DES remains in many products — and cryptography students and cryptographers will continue to study DES for years to come.
DES Operational Overview
DES uses a 56-bit key. In fact, the 56-bit key is divided into eight 7-bit blocks and an 8th odd parity bit is added to each block (i.e., a "0" or "1" is added to the block so that there are an odd number of 1 bits in each 8-bit block). By using the 8 parity bits for rudimentary error detection, a DES key is actually 64 bits in length for computational purposes although it only has 56 bits worth of randomness, or entropy (See Section A.3 for a brief discussion of entropy and information theory).

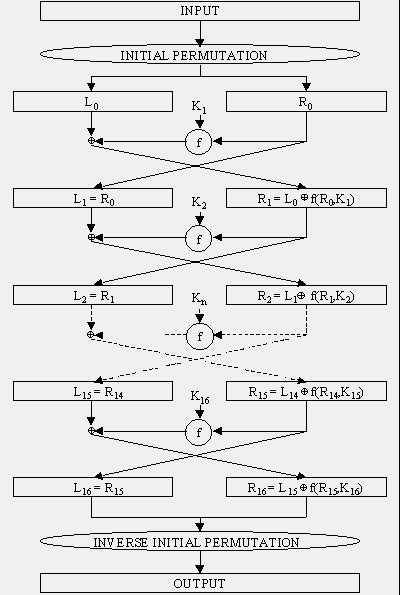
FIGURE 6: DES enciphering algorithm.

DES then acts on 64-bit blocks of the plaintext, invoking 16 rounds of permutations, swaps, and substitutes, as shown in Figure 6. The standard includes tables describing all of the selection, permutation, and expansion operations mentioned below; these aspects of the algorithm are not secrets. The basic DES steps are:

1. The 64-bit block to be encrypted undergoes an initial permutation (IP), where each bit is moved to a new bit position; e.g., the 1st, 2nd, and 3rd bits are moved to the 58th, 50th, and 42nd position, respectively.
   
   
2. The 64-bit permuted input is divided into two 32-bit blocks, called left and right, respectively. The initial values of the left and right blocks are denoted L₀ and R₀.
   
   
3. There are then 16 rounds of operation on the L and R blocks. During each iteration (where n ranges from 1 to 16), the following formulae apply:
   L_n = R_n-1
   R_n = L_n-1 XOR f(R_n-1,K_n)
   At any given step in the process, then, the new L block value is merely taken from the prior R block value. The new R block is calculated by taking the bit-by-bit exclusive-OR (XOR) of the prior L block with the results of applying the DES cipher function, f, to the prior R block and K_n. (K_n is a 48-bit value derived from the 64-bit DES key. Each round uses a different 48 bits according to the standard's Key Schedule algorithm.) The cipher function, f, combines the 32-bit R block value and the 48-bit subkey in the following way. First, the 32 bits in the R block are expanded to 48 bits by an expansion function (E); the extra 16 bits are found by repeating the bits in 16 predefined positions. The 48-bit expanded R-block is then ORed with the 48-bit subkey. The result is a 48-bit value that is then divided into eight 6-bit blocks. These are fed as input into 8 selection (S) boxes, denoted S₁,...,S₈. Each 6-bit input yields a 4-bit output using a table lookup based on the 64 possible inputs; this results in a 32-bit output from the S-box. The 32 bits are then rearranged by a permutation function (P), producing the results from the cipher function.
   
   
4. The results from the final DES round — i.e., L₁₆ and R₁₆ — are recombined into a 64-bit value and fed into an inverse initial permutation (IP^-1). At this step, the bits are rearranged into their original positions, so that the 58th, 50th, and 42nd bits, for example, are moved back into the 1st, 2nd, and 3rd positions, respectively. The output from IP^-1 is the 64-bit ciphertext block.

Consider this example with the given 56-bit key and input:

Key: 1100101 0100100 1001001 0011101 0110101 0101011 1101100 0011010

Input character string:  GoAggies
Input bit string:  11100010 11110110 10000010 11100110 11100110 10010110 10100110 11001110

Output bit string: 10011111 11110010 10000000 10000001 01011011 00101001 00000011 00101111
Output character string: ùO Ú”Àô

Breaking DES
The mainstream cryptographic community has long held that DES's 56-bit key was too short to withstand a brute-force attack from modern computers. Remember Moore's Law: computer power doubles every 18 months. Given that increase in power, a key that could withstand a brute-force guessing attack in 1975 could hardly be expected to withstand the same attack a quarter century later.
DES is even more vulnerable to a brute-force attack because it is often used to encrypt words, meaning that the entropy of the 64-bit block is, effectively, greatly reduced. That is, if we are encrypting random bit streams, then a given byte might contain any one of 2⁸ (256) possible values and the entire 64-bit block has 2⁶⁴, or about 18.5 quintillion, possible values. If we are encrypting words, however, we are most likely to find a limited set of bit patterns; perhaps 70 or so if we account for upper and lower case letters, the numbers, space, and some punctuation. This means that only about ¼ of the bit combinations of a given byte are likely to occur.
Despite this criticism, the U.S. government insisted throughout the mid-1990s that 56-bit DES was secure and virtually unbreakable if appropriate precautions were taken. In response, RSA Laboratories sponsored a series of cryptographic challenges to prove that DES was no longer appropriate for use.
DES Challenge I was launched in March 1997. It was completed in 84 days by R. Verser in a collaborative effort using thousands of computers on the Internet.
The first DES II challenge lasted 40 days in early 1998. This problem was solved by distributed.net, a worldwide distributed computing network using the spare CPU cycles of computers around the Internet (participants in distributed.net's activities load a client program that runs in the background, conceptually similar to the SETI @Home "Search for Extraterrestrial Intelligence" project). The distributed.net systems were checking 28 billion keys per second by the end of the project.
The second DES II challenge lasted less than 3 days. On July 17, 1998, the Electronic Frontier Foundation (EFF) announced the construction of hardware that could brute-force a DES key in an average of 4.5 days. Called Deep Crack, the device could check 90 billion keys per second and cost only about $220,000 including design (it was erroneously and widely reported that subsequent devices could be built for as little as $50,000). Since the design is scalable, this suggests that an organization could build a DES cracker that could break 56-bit keys in an average of a day for as little as $1,000,000. Information about the hardware design and all software can be obtained from the EFF.
The DES III challenge, launched in January 1999, was broken is less than a day by the combined efforts of Deep Crack and distributed.net. This is widely considered to have been the final nail in DES's coffin.
The Deep Crack algorithm is actually quite interesting. The general approach that the DES Cracker Project took was not to break the algorithm mathematically but instead to launch a brute-force attack by guessing every possible key. A 56-bit key yields 2⁵⁶, or about 72 quadrillion, possible values. So the DES cracker team looked for any shortcuts they could find! First, they assumed that some recognizable plaintext would appear in the decrypted string even though they didn't have a specific known plaintext block. They then applied all 2⁵⁶ possible key values to the 64-bit block (I don't mean to make this sound simple!). The system checked to see if the decrypted value of the block was "interesting," which they defined as bytes containing one of the alphanumeric characters, space, or some punctuation. Since the likelihood of a single byte being "interesting" is about ¼, then the likelihood of the entire 8-byte stream being "interesting" is about ¼⁸, or 1/65536 (½¹⁶). This dropped the number of possible keys that might yield positive results to about 2⁴⁰, or about a trillion.
They then made the assumption that an "interesting" 8-byte block would be followed by another "interesting" block. So, if the first block of ciphertext decrypted to something interesting, they decrypted the next block; otherwise, they abandoned this key. Only if the second block was also "interesting" did they examine the key closer. Looking for 16 consecutive bytes that were "interesting" meant that only 2²⁴, or 16 million, keys needed to be examined further. This further examination was primarily to see if the text made any sense. Note that possible "interesting" blocks might be 1hJ5&aB7 or DEPOSITS; the latter is more likely to produce a better result. And even a slow laptop today can search through lists of only a few million items in a relatively short period of time. (Interested readers are urged to read Cracking DES and EFF's Cracking DES page.)
It is well beyond the scope of this paper to discuss other forms of breaking DES and other codes. Nevertheless, it is worth mentioning a couple of forms of cryptanalysis that have been shown to be effective against DES. Differential cryptanalysis, invented in 1990 by E. Biham and A. Shamir (of RSA fame), is a chosen-plaintext attack. By selecting pairs of plaintext with particular differences, the cryptanalyst examines the differences in the resultant ciphertext pairs. Linear plaintext, invented by M. Matsui, uses a linear approximation to analyze the actions of a block cipher (including DES). Both of these attacks can be more efficient than brute force.
DES Variants
Once DES was "officially" broken, several variants appeared. But none of them came overnight; work at hardening DES had already been underway. In the early 1990s, there was a proposal to increase the security of DES by effectively increasing the key length by using multiple keys with multiple passes. But for this scheme to work, it had to first be shown that the DES function is not a group, as defined in mathematics. If DES was a group, then we could show that for two DES keys, X1 and X2, applied to some plaintext (P), we can find a single equivalent key, X3, that would provide the same result; i.e.,:

E_X2(E_X1(P)) = E_X3(P)

where E_X(P) represents DES encryption of some plaintext P using DES key X. If DES were a group, it wouldn't matter how many keys and passes we applied to some plaintext; we could always find a single 56-bit key that would provide the same result.
As it happens, DES was proven to not be a group so that as we apply additional keys and passes, the effective key length increases. One obvious choice, then, might be to use two keys and two passes, yielding an effective key length of 112 bits. Let's call this Double-DES. The two keys, Y1 and Y2, might be applied as follows:

C = E_Y2(E_Y1(P))
P = D_Y1(D_Y2(C))

where E_Y(P) and D_Y(C) represent DES encryption and decryption, respectively, of some plaintext P and ciphertext C, respectively, using DES key Y.
So far, so good. But there's an interesting attack that can be launched against this "Double-DES" scheme. First, notice that the applications of the formula above can be thought of with the following individual steps (where C' and P' are intermediate results):

C' = E_Y1(P) and C = E_Y2(C')
P' = D_Y2(C) and P = D_Y1(P')

Unfortunately, C'=P'. That leaves us vulnerable to a simple known plaintext attack (sometimes called "Meet-in-the-middle") where the attacker knows some plaintext (P) and its matching ciphertext (C). To obtain C', the attacker needs to try all 2⁵⁶ possible values of Y1 applied to P; to obtain P', the attacker needs to try all 2⁵⁶ possible values of Y2 applied to C. Since C'=P', the attacker knows when a match has been achieved — after only 2⁵⁶ + 2⁵⁶ = 2⁵⁷ key searches, only twice the work of brute-forcing DES. So "Double-DES" won't work.
Triple-DES (3DES), based upon the Triple Data Encryption Algorithm (TDEA), is described in FIPS 46-3. 3DES, which is not susceptible to a meet-in-the-middle attack, employs three DES passes and one, two, or three keys called K1, K2, and K3. Generation of the ciphertext (C) from a block of plaintext (P) is accomplished by:

C = E_K3(D_K2(E_K1(P)))

where E_K(P) and D_K(P) represent DES encryption and decryption, respectively, of some plaintext P using DES key K. (For obvious reasons, this is sometimes referred to as an encrypt-decrypt-encrypt mode operation.)
Decryption of the ciphertext into plaintext is accomplished by:

P = D_K1(E_K2(D_K3(C)))

The use of three, independent 56-bit keys provides 3DES with an effective key length of 168 bits. The specification also defines use of two keys where, in the operations above, K3 = K1; this provides an effective key length of 112 bits. Finally, a third keying option is to use a single key, so that K3 = K2 = K1 (in this case, the effective key length is 56 bits and 3DES applied to some plaintext, P, will yield the same ciphertext, C, as normal DES would with that same key). Given the relatively low cost of key storage and the modest increase in processing due to the use of longer keys, the best recommended practices are that 3DES be employed with three keys.
Another variant of DES, called DESX, is due to Ron Rivest. Developed in 1996, DESX is a very simple algorithm that greatly increases DES's resistance to brute-force attacks without increasing its computational complexity. In DESX, the plaintext input is XORed with 64 additional key bits prior to encryption and the output is likewise XORed with the 64 key bits. By adding just two XOR operations, DESX has an effective keylength of 120 bits against an exhaustive key-search attack. As it happens, DESX is no more immune to other types of more sophisticated attacks, such as differential or linear cryptanalysis, but brute-force is the primary attack vector on DES.
Closing Comments
Although DES has been deprecated and replaced by the Advanced Encryption Standard (AES) because of its vulnerability to a modestly-priced brute-force attack, many applications continue to rely on DES for security, and many software designers and implementers continue to include DES in new applications. In some cases, use of DES is wholly appropriate but, in general, DES should not continue to be promulgated in production software and hardware. RFC 4772 discusses the security implications of employing DES.
On a final note, readers may be interested in seeing The Illustrated DES Spreadsheet (J. Hughes, 2004), an Excel implementation of DES, or J.O. Grabbe's The DES Algorithm Illustrated.

5.5. Pretty Good Privacy (PGP)

Pretty Good Privacy (PGP) is one of today's most widely used public key cryptography programs. Developed by Philip Zimmermann in the early 1990s and long the subject of controversy, PGP is available as a plug-in for many e-mail clients, such as Claris Emailer, Microsoft Outlook/Outlook Express, and Qualcomm Eudora.
PGP can be used to sign or encrypt e-mail messages with the mere click of the mouse. Depending upon the version of PGP, the software uses SHA or MD5 for calculating the message hash; CAST, Triple-DES, or IDEA for encryption; and RSA or DSS/Diffie-Hellman for key exchange and digital signatures.
When PGP is first installed, the user has to create a key-pair. One key, the public key, can be advertised and widely circulated. The private key is protected by use of a passphrase. The passphrase has to be entered every time the user accesses their private key.

-----BEGIN PGP SIGNED MESSAGE----- Hash: SHA1 Hi Carol. What was that pithy Groucho Marx quote? /kess -----BEGIN PGP SIGNATURE----- Version: PGP for Personal Privacy 5.0 Charset: noconv iQA/AwUBNFUdO5WOcz5SFtuEEQJx/ACaAgR97+vvDU6XWELV/GANjAAgBtUAnjG3 Sdfw2JgmZIOLNjFe7jP0Y8/M =jUAU -----END PGP SIGNATURE----- FIGURE 7: A PGP signed message. The sender uses their private key; at the destination, the sender's e-mail address yields the public key from the receiver's keyring.

Figure 7 shows a PGP signed message. This message will not be kept secret from an eavesdropper, but a recipient can be assured that the message has not been altered from what the sender transmitted. In this instance, the sender signs the message using their own private key. The receiver uses the sender's public key to verify the signature; the public key is taken from the receiver's keyring based on the sender's e-mail address. Note that the signature process does not work unless the sender's public key is on the receiver's keyring.

-----BEGIN PGP MESSAGE----- Version: PGP for Personal Privacy 5.0 MessageID: DAdVB3wzpBr3YRunZwYvhK5gBKBXOb/m qANQR1DBwU4D/TlT68XXuiUQCADfj2o4b4aFYBcWumA7hR1Wvz9rbv2BR6WbEUsy ZBIEFtjyqCd96qF38sp9IQiJIKlNaZfx2GLRWikPZwchUXxB+AA5+lqsG/ELBvRa c9XefaYpbbAZ6z6LkOQ+eE0XASe7aEEPfdxvZZT37dVyiyxuBBRYNLN8Bphdr2zv z/9Ak4/OLnLiJRk05/2UNE5Z0a+3lcvITMmfGajvRhkXqocavPOKiin3hv7+Vx88 uLLem2/fQHZhGcQvkqZVqXx8SmNw5gzuvwjV1WHj9muDGBY0MkjiZIRI7azWnoU9 3KCnmpR60VO4rDRAS5uGl9fioSvze+q8XqxubaNsgdKkoD+tB/4u4c4tznLfw1L2 YBS+dzFDw5desMFSo7JkecAS4NB9jAu9K+f7PTAsesCBNETDd49BTOFFTWWavAfE gLYcPrcn4s3EriUgvL3OzPR4P1chNu6sa3ZJkTBbriDoA3VpnqG3hxqfNyOlqAka mJJuQ53Ob9ThaFH8YcE/VqUFdw+bQtrAJ6NpjIxi/x0FfOInhC/bBw7pDLXBFNaX HdlLQRPQdrmnWskKznOSarxq4GjpRTQo4hpCRJJ5aU7tZO9HPTZXFG6iRIT0wa47 AR5nvkEKoIAjW5HaDKiJriuWLdtN4OXecWvxFsjR32ebz76U8aLpAK87GZEyTzBx dV+lH0hwyT/y1cZQ/E5USePP4oKWF4uqquPee1OPeFMBo4CvuGyhZXD/18Ft/53Y WIebvdiCqsOoabK3jEfdGExce63zDI0= =MpRf -----END PGP MESSAGE----- FIGURE 8: A PGP encrypted message. The receiver's e-mail address is the pointer to the public key in the sender's keyring. At the destination side, the receiver uses their own private key.

Figure 8 shows a PGP encrypted message (PGP compresses the file, where practical, prior to encryption because encrypted files have a high degree of randomness and, therefore, cannot be efficiently compressed). In this example, public key methods are used to exchange the session key for the actual message encryption that employs secret-key cryptography. In this case, the receiver's e-mail address is the pointer to the public key in the sender's keyring; in fact, the same message can be sent to multiple recipients and the message will not be significantly longer since all that needs to be added is the session key encrypted by each receiver's public key. When the message is received, the recipient will use their private key to extract the session secret key to successfully decrypt the message (Figure 9).

Hi Gary, "Outside of a dog, a book is man's best friend. Inside of a dog, it's too dark to read." Carol FIGURE 9: The decrypted message.

It is worth noting that PGP was one of the first so-called "hybrid cryptosystems" that combined aspects of SKC and PKC. When Zimmermann was first designing PGP in the late-1980s, he wanted to use RSA to encrypt the entire message. The PCs of the days, however, suffered significant performance degradation when executing RSA so he hit upon the idea of using SKC to encrypt the message and PKC to encrypt the SKC key.
PGP went into a state of flux in 2002. Zimmermann sold PGP to Network Associates, Inc. (NAI) in 1997 and himself resigned from NAI in early 2001. In March 2002, NAI announced that they were dropping support for the commercial version of PGP having failed to find a buyer for the product willing to pay what NAI wanted. In August 2002, PGP was purchased from NAI by PGP Corp. (http://www.pgp.com/). Meanwhile, there are many freeware versions of PGP available through the International PGP Page and the OpenPGP Alliance. Also check out the GNU Privacy Guard (GnuPG), a GNU project implementation of OpenPGP (defined in RFC 2440).

5.6. IP Security (IPsec) Protocol

NOTE: The information in this section assumes that the reader is familiar with the Internet Protocol (IP), at least to the extent of the packet format and header contents. More information about IP can be found in An Overview of TCP/IP Protocols and the Internet. More information about IPv6 can be found in IPv6: The Next Generation Internet Protocol.

The Internet and the TCP/IP protocol suite were not built with security in mind. This statement is not meant as a criticism; the baseline UDP, TCP, IP, and ICMP protocols were written in 1980 and built for the relatively closed ARPANET community. TCP/IP wasn't designed for the commercial-grade financial transactions that they now see nor for virtual private networks (VPNs) on the Internet. To bring TCP/IP up to today's security necessities, the Internet Engineering Task Force (IETF) formed the IP Security Protocol Working Group which, in turn, developed the IP Security (IPsec) protocol. IPsec is not a single protocol, in fact, but a suite of protocols providing a mechanism to provide data integrity, authentication, privacy, and nonrepudiation for the classic Internet Protocol (IP). Although intended primarily for IP version 6 (IPv6), IPsec can also be employed by the current version of IP, namely IP version 4 (IPv4).
As shown in Table 3, IPsec is described in nearly a dozen RFCs. RFC 4301, in particular, describes the overall IP security architecture and RFC 2411 provides an overview of the IPsec protocol suite and the documents describing it.
IPsec can provide either message authentication and/or encryption. The latter requires more processing than the former, but will probably end up being the preferred usage for applications such as VPNs and secure electronic commerce.
Central to IPsec is the concept of a security association (SA). Authentication and confidentiality using AH or ESP use SAs and a primary role of IPsec key exchange it to establish and maintain SAs. An SA is a simplex (one-way or unidirectional) logical connection between two communicating IP endpoints that provides security services to the traffic carried by it using either AH or ESP procedures. The endpoint of an SA can be an IP host or IP security gateway (e.g., a proxy server, VPN server, etc.). Providing security to the more typical scenario of two-way (bi-directional) communication between two endpoints requires the establishment of two SAs (one in each direction).
An SA is uniquely identified by a 3-tuple composed of:

• Security Parameter Index (SPI), a 32-bit identifier of the connection
• IP Destination Address
• security protocol (AH or ESP) identifier

The IP Authentication Header (AH), described in RFC 4302, provides a mechanism for data integrity and data origin authentication for IP packets using HMAC with MD5 (RFC 2403), HMAC with SHA-1 (RFC 2404), or HMAC with RIPEMD (RFC 2857). See also RFC 4305.

0 1 2 3 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | Next Header | Payload Len | RESERVED | +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | Security Parameters Index (SPI) | +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | Sequence Number Field | +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | | + Integrity Check Value-ICV (variable) | | | +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ FIGURE 10: IPsec Authentication Header format. (From RFC 4302)

Figure 10 shows the format of the IPsec AH. The AH is merely an additional header in a packet, more or less representing another protocol layer above IP (this is shown in Figure 12 below). Use of the IP AH is indicated by placing the value 51 (0x33) in the IPv4 Protocol or IPv6 Next Header field in the IP packet header. The AH follows mandatory IPv4/IPv6 header fields and precedes higher layer protocol (e.g., TCP, UDP) information. The contents of the AH are:

• Next Header: An 8-bit field that identifies the type of the next payload after the Authentication Header.
• Payload Length: An 8-bit field that indicates the length of AH in 32-bit words (4-byte blocks), minus "2". [The rationale for this is somewhat counter intuitive but technically important. All IPv6 extension headers encode the header extension length (Hdr Ext Len) field by first subtracting 1 from the header length, which is measured in 64-bit words. Since AH was originally developed for IPv6, it is an IPv6 extension header. Since its length is measured in 32-bit words, however, the Payload Length is calculated by subtracting 2 (32 bit words) to maintain consistency with IPv6 coding rules.] In the default case, the three 32-bit word fixed portion of the AH is followed by a 96-bit authentication value, so the Payload Length field value would be 4.
• Reserved: This 16-bit field is reserved for future use and always filled with zeros.
• Security Parameters Index (SPI): An arbitrary 32-bit value that, in combination with the destination IP address and security protocol, uniquely identifies the Security Association for this datagram. The value 0 is reserved for local, implementation-specific uses and values between 1-255 are reserved by the Internet Assigned Numbers Authority (IANA) for future use.
• Sequence Number: A 32-bit field containing a sequence number for each datagram; initially set to 0 at the establishment of an SA. AH uses sequence numbers as an anti-replay mechanism, to prevent a "person-in-the-middle" attack. If anti-replay is enabled (the default), the transmitted Sequence Number is never allowed to cycle back to 0; therefore, the sequence number must be reset to 0 by establishing a new SA prior to the transmission of the 2³²nd packet.
• Authentication Data: A variable-length, 32-bit aligned field containing the Integrity Check Value (ICV) for this packet (default length = 96 bits). The ICV is computed using the authentication algorithm specified by the SA, such as DES, MD5, or SHA-1. Other algorithms may also be supported.

The IP Encapsulating Security Payload (ESP), described in RFC 4303, provides message integrity and privacy mechanisms in addition to authentication. As in AH, ESP uses HMAC with MD5, SHA-1, or RIPEMD authentication (RFC 2403/RFC 2404/RFC 2857); privacy is provided using DES-CBC encryption (RFC 2405), NULL encryption (RFC 2410), other CBC-mode algorithms (RFC 2451), or AES (RFC 3686). See also RFC 4305 and RFC 4308.

0 1 2 3 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ ---- | Security Parameters Index (SPI) | ^Int. +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ |Cov- | Sequence Number | |ered +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | ---- | Payload Data* (variable) | | ^ ~ ~ | | | | |Conf. + +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ |Cov- | | Padding (0-255 bytes) | |ered* +-+-+-+-+-+-+-+-+ +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ | | | | Pad Length | Next Header | v v +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ ------ | Integrity Check Value-ICV (variable) | ~ ~ | | +-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+ * If included in the Payload field, cryptographic synchronization data, e.g., an Initialization Vector (IV), usually is not encrypted per se, although it often is referred to as being being part of the ciphertext. FIGURE 11: IPsec Encapsulating Security Payload format. (From RFC 4303)

Figure 11 shows the format of the IPsec ESP information. Use of the IP ESP format is indicated by placing the value 50 (0x32) in the IPv4 Protocol or IPv6 Next Header field in the IP packet header. The ESP header (i.e., SPI and sequence number) follows mandatory IPv4/IPv6 header fields and precedes higher layer protocol (e.g., TCP, UDP) information. The contents of the ESP packet are:

• Security Parameters Index: (see description for this field in the AH, above.)
• Sequence Number: (see description for this field in the AH, above.)
• Payload Data: A variable-length field containing data as described by the Next Header field. The contents of this field could be encrypted higher layer data or an encrypted IP packet.
• Padding: Between 0 and 255 octets of padding may be added to the ESP packet. There are several applications that might use the padding field. First, the encryption algorithm that is used may require that the plaintext be a multiple of some number of bytes, such as the block size of a block cipher; in this case, the Padding field is used to fill the plaintext to the size required by the algorithm. Second, padding may be required to ensure that the ESP packet and resulting ciphertext terminate on a 4-byte boundary. Third, padding may be used to conceal the actual length of the payload. Unless another value is specified by the encryption algorithm, the Padding octets take on the value 1, 2, 3, ... starting with the first Padding octet. This scheme is used because, in addition to being simple to implement, it provides some protection against certain forms of "cut and paste" attacks.
• Pad Length: An 8-bit field indicating the number of bytes in the Padding field; contains a value between 0-255.
• Next Header: An 8-bit field that identifies the type of data in the Payload Data field, such as an IPv6 extension header or a higher layer protocol identifier.
• Authentication Data: (see description for this field in the AH, above.)

Two types of SAs are defined in IPsec, regardless of whether AH or ESP is employed. A transport mode SA is a security association between two hosts. Transport mode provides the authentication and/or encryption service to the higher layer protocol. This mode of operation is only supported by IPsec hosts. A tunnel mode SA is a security association applied to an IP tunnel. In this mode, there is an "outer" IP header that specifies the IPsec destination and an "inner" IP header that specifies the destination for the IP packet. This mode of operation is supported by both hosts and security gateways.

ORIGINAL PACKET BEFORE APPLYING AH ---------------------------- IPv4 |orig IP hdr | | | |(any options)| TCP | Data | ---------------------------- --------------------------------------- IPv6 | | ext hdrs | | | | orig IP hdr |if present| TCP | Data | --------------------------------------- AFTER APPLYING AH (TRANSPORT MODE) ------------------------------------------------------- IPv4 |original IP hdr (any options) | AH | TCP | Data | ------------------------------------------------------- |<- mutable field processing ->|<- immutable fields ->| |<----- authenticated except for mutable fields ----->| ------------------------------------------------------------ IPv6 | |hop-by-hop, dest*, | | dest | | | |orig IP hdr |routing, fragment. | AH | opt* | TCP | Data | ------------------------------------------------------------ |<--- mutable field processing -->|<-- immutable fields -->| |<---- authenticated except for mutable fields ----------->| * = if present, could be before AH, after AH, or both AFTER APPLYING AH (TUNNEL MODE) ---------------------------------------------------------------- IPv4 | | | orig IP hdr* | | | |new IP header * (any options) | AH | (any options) |TCP| Data | ---------------------------------------------------------------- |<- mutable field processing ->|<------ immutable fields ----->| |<- authenticated except for mutable fields in the new IP hdr->| -------------------------------------------------------------- IPv6 | | ext hdrs*| | | ext hdrs*| | | |new IP hdr*|if present| AH |orig IP hdr*|if present|TCP|Data| -------------------------------------------------------------- |<--- mutable field -->|<--------- immutable fields -------->| | processing | |<-- authenticated except for mutable fields in new IP hdr ->| * = if present, construction of outer IP hdr/extensions and modification of inner IP hdr/extensions is discussed in the Security Architecture document. FIGURE 12: IPsec tunnel and transport modes for AH. (Adapted from RFC 4302)

Figure 12 show the IPv4 and IPv6 packet formats when using AH in both transport and tunnel modes. Initially, an IPv4 packet contains a normal IPv4 header (which may contain IP options), followed by the higher layer protocol header (e.g., TCP or UDP), followed by the higher layer data itself. An IPv6 packet is similar except that the packet starts with the mandatory IPv6 header followed by any IPv6 extension headers, and then followed by the higher layer data.
Note that in both transport and tunnel modes, the entire IP packet is covered by the authentication except for the mutable fields. A field is mutable if its value might change during transit in the network; IPv4 mutable fields include the fragment offset, time to live, and checksum fields. Note, in particular, that the address fields are not mutable.

ORIGINAL PACKET BEFORE APPLYING ESP ---------------------------- IPv4 |orig IP hdr | | | |(any options)| TCP | Data | ---------------------------- --------------------------------------- IPv6 | | ext hdrs | | | | orig IP hdr |if present| TCP | Data | --------------------------------------- AFTER APPLYING ESP (TRANSPORT MODE) ------------------------------------------------- IPv4 |orig IP hdr | ESP | | | ESP | ESP| |(any options)| Hdr | TCP | Data | Trailer | ICV| ------------------------------------------------- |<---- encryption ---->| |<-------- integrity ------->| --------------------------------------------------------- IPv6 | orig |hop-by-hop,dest*,| |dest| | | ESP | ESP| |IP hdr|routing,fragment.|ESP|opt*|TCP|Data|Trailer| ICV| --------------------------------------------------------- |<--- encryption ---->| |<------ integrity ------>| * = if present, could be before ESP, after ESP, or both AFTER APPLYING ESP (TUNNEL MODE) ----------------------------------------------------------- IPv4 | new IP hdr+ | | orig IP hdr+ | | | ESP | ESP| |(any options)| ESP | (any options) |TCP|Data|Trailer| ICV| ----------------------------------------------------------- |<--------- encryption --------->| |<------------- integrity ------------>| ------------------------------------------------------------ IPv6 | new+ |new ext | | orig+|orig ext | | | ESP | ESP| |IP hdr| hdrs+ |ESP|IP hdr| hdrs+ |TCP|Data|Trailer| ICV| ------------------------------------------------------------ |<--------- encryption ---------->| |<------------ integrity ------------>| + = if present, construction of outer IP hdr/extensions and modification of inner IP hdr/extensions is discussed in the Security Architecture document. FIGURE 13: IPsec tunnel and transport modes for ESP. (Adapted from RFC 4303)

Figure 13 shows the IPv4 and IPv6 packet formats when using ESP in both transport and tunnel modes.

• As with AH, we start with a standard IPv4 or IPv6 packet.
• In transport mode, the higher layer header and data, as well as ESP trailer information, is encrypted and the entire ESP packet is authenticated. In the case of IPv6, some of the IPv6 extension options can precede or follow the ESP header.
• In tunnel mode, the original IP packet is encrypted and placed inside of an "outer" IP packet, while the entire ESP packet is authenticated.

Note a significant difference in the scope of ESP and AH. AH authenticates the entire packet transmitted on the network whereas ESP only covers a portion of the packet transmitted on the network (the higher layer data in transport mode and the entire original packet in tunnel mode). The reason for this is straight-forward; in AH, the authentication data for the transmission fits neatly into an additional header whereas ESP creates an entirely new packet which is the one encrypted and/or authenticated. But the ramifications are significant. ESP transport mode as well as AH in both modes protect the IP address fields of the original transmissions. Thus, using IPsec in conjunction with network address translation (NAT) might be problematic because NAT changes the values of these fields after IPsec processing.
The third component of IPsec is the establishment of security associations and key management. These tasks can be accomplished in one of two ways.
The simplest form of SA and key management is manual management. In this method, a security administer or other individual manually configures each system with the key and SA management data necessary for secure communication with other systems. Manual techniques are practical for small, reasonably static environments but they do not scale well.
For successful deployment of IPsec, however, a scalable, automated SA/key management scheme is necessary. Several protocols have defined for these functions:

• The Internet Security Association and Key Management Protocol (ISAKMP) defines procedures and packet formats to establish, negotiate, modify and delete security associations, and provides the framework for exchanging information about authentication and key management (RFC 2407/RFC 2408). ISAKMP's security association and key management is totally separate from key exchange.
• The OAKLEY Key Determination Protocol (RFC 2412) describes a scheme by which two authenticated parties can exchange key information. OAKLEY uses the Diffie-Hellman key exchange algorithm.
• The Internet Key Exchange (IKE) algorithm (RFC 2409) is the default automated key management protocol for IPsec.
• An alternative to IKE is Photuris (RFC 2522/RFC 2523), a scheme for establishing short-lived session-keys between two authenticated parties without passing the session-keys across the Internet. IKE typically creates keys that may have very long lifetimes.

On a final note, IPsec authentication for both AH and ESP uses a scheme called HMAC, a keyed-hashing message authentication code described in FIPS 198 and RFC 2104. HMAC uses a shared secret key between two parties rather than public key methods for message authentication. The generic HMAC procedure can be used with just about any hash algorithm, although IPsec specifies support for at least MD5 and SHA-1 because of their widespread use.
In HMAC, both parties share a secret key. The secret key will be employed with the hash algorithm in a way that provides mutual authentication without transmitting the key on the line. IPsec key management procedures will be used to manage key exchange between the two parties.
Recall that hash functions operate on a fixed-size block of input at one time; MD5 and SHA-1, for example, work on 64 byte blocks. These functions then generate a fixed-size hash value; MD5 and SHA-1, in particular, produce 16 byte (128 bit) and 20 byte (160 bit) output strings, respectively. For use with HMAC, the secret key (K) should be at least as long as the hash output.
The following steps provide a simplified, although reasonably accurate, description of how the HMAC scheme would work with a particular plaintext MESSAGE:

1. Alice pads K so that it is as long as an input block; call this padded key K_p. Alice computes the hash of the padded key followed by the message, i.e., HASH (K_p:MESSAGE).
2. Alice transmits MESSAGE and the hash value.
3. Bob has also padded K to create K_p. He computes HASH (K_p:MESSAGE) on the incoming message.
4. Bob compares the computed hash value with the received hash value. If they match, then the sender — Alice — must know the secret key and the message is authenticated.

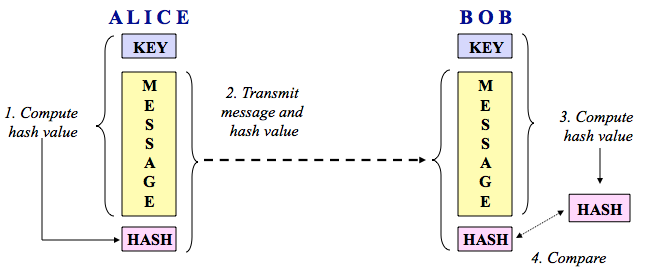
FIGURE 14: Keyed-hash MAC operation.

5.7. The SSL Family of Secure Transaction Protocols for the World Wide Web

The Secure Sockets Layer (SSL) protocol was developed by Netscape Communications to provide application-independent secure communication over the Internet for protocols such as the Hypertext Transfer Protocol (HTTP). SSL employs RSA and X.509 certificates during an initial handshake used to authenticate the server (client authentication is optional). The client and server then agree upon an encryption scheme. SSL v2.0 (1995), the first version publicly released, supported RC2 and RC4 with 40-bit keys. SSL v3.0 (1996) added support for DES, RC4 with a 128-bit key, and 3DES with a 168-bit key, all along with either MD5 or SHA-1 message hashes; this protocol is described in RFC 6101.

FIGURE 15: Browser encryption configuration screen (Firefox).

In 1997, SSL v3 was found to be breakable. By this time, the Internet Engineering Task Force (IETF) had already started work on a new, non-proprietary protocol called Transport Layer Security (TLS), described in RFC 2246 (1999). TLS extends SSL and supports additional crypto schemes, such as Diffie-Hellman key exchange and DSS digital signatures; RFC 4279 describes the pre-shared key crypto schemes supported by TLS. TLS is backward compatible with SSL (and, in fact, is recognized as SSL v3.1). SSL v3.0 and TLS v1.0 are the commonly supported versions on servers and browsers today (Figure 15); SSL v2.0 is rarely found today and, in fact, RFC 6176-compliant client and servers that support TLS will never negotiate the use of SSL v2.
In 2002, a cipher block chaining (CBC) vulnerability was described for TLS v1.0. In 2011, the theoretical became practical when a CBC proof-of-concept exploit was released. Meanwhile, TLS v1.1 was defined in 2006 (RFC 4346), adding protection against v1.0's CBC vulnerability. In 2008, TLS v1.2 was defined (RFC 5246), adding several additional cryptographic options. Today, users are urged to use TLS v1.2 or v1.1 in lieu of any earlier versions.

CLIENT SERVER (using URL of form https://) (listening on port 443) ClientHello ----> ServerHello Certificate* ServerKeyExchange* CertificateRequest* <---- ServerHelloDone Certificate* ClientKeyExchange CertifcateVerify* [ChangeCipherSpec] Finished ----> [ChangeCipherSpec] <---- Finished Application Data <---> Application Data * Optional or situation-dependent messages; not always sent Adapted from RFC 2246 FIGURE 16: SSL/TLS protocol handshake.

Figure 16 shows the basic TLS (and SSL) message exchanges:

1. URLs specifying the protocol https:// are directed to HTTP servers secured using SSL/TLS. The client will automatically try to make a TCP connection to the server at port 443. The client initiates the secure connection by sending a ClientHello message containing a Session identifier, highest SSL version number supported by the client, and lists of supported crypto and compression schemes (in preference order).
2. The server examines the Session ID and if it is still in the server's cache, it will attempt to re-establish a previous session with this client. If the Session ID is not recognized, the server will continue with the handshake to establish a secure session by responding with a ServerHello message. The ServerHello repeats the Session ID, indicates the SSL version to use for this connection (which will be the highest SSL version supported by the server and client), and specifies which encryption method and compression method to be used for this connection.
3. There are a number of other optional messages that the server might send, including:
   • Certificate, which carries the server's X.509 public key certificate (and, generally, the server's public key). This message will always be sent unless the client and server have already agreed upon some form of anonymous key exchange. (This message is normally sent.)
   • ServerKeyExchange, which will carry a premaster secret when the server's Certificate message does not contain enough data for this purpose; used in some key exchange schemes.
   • CertificateRequest, used to request the client's certificate in those scenarios where client authentication is performed.
   • ServerHelloDone, indicating that the server has completed its portion of the key exchange handshake.
4. The client now responds with a series of mandatory and optional messages:
   • Certificate, contains the client's public key certificate when it has been requested by the server.
   • ClientKeyExchange, which usually carries the secret key to be used with the secret key crypto scheme.
   • CertificateVerify, used to provide explicit verification of a client's certificate if the server is authenticating the client.
5. TLS includes the change cipher spec protocol to indicate changes in the encryption method. This protocol contains a single message, ChangeCipherSpec, which is encrypted and compressed using the current (rather than the new) encryption and compression schemes. The ChangeCipherSpec message is sent by both client and server to notify the other station that all following information will employ the newly negotiated cipher spec and keys.
6. The Finished message is sent after a ChangeCipherSpec message to confirm that the key exchange and authentication processes were successful.
7. At this point, both client and server can exchange application data using the session encryption and compression schemes. Side Note: It would probably be helpful to make some mention of SSL (or, more properly, TLS) as it is used today. Most of us have used SSL to engage in a secure, private transaction with some vendor. The steps are something like this. During the SSL exchange with the vendor's secure server, the server sends its certificate to our client software. The certificate includes the vendor's public key and a signature from the CA that issued the vendor's certificate. Our browser software is shipped with the major CAs' certificates which contains their public key; in that way we authenticate the server. Note that the server does not use a certificate to authenticate us! Instead, we are generally authenticated when we provide our credit card number; the server checks to see if the card purchase will be authorized by the credit card company and, if so, considers us valid and authenticated! While bidirectional authentication is certainly supported by SSL, this form of asymmetric authentication is more commonly employed today since most users don't have certificates.
   Microsoft's Server Gated Cryptography (SGC) protocol is another extension to SSL/TLS. For several decades, it has been illegal to generally export products from the U.S. that employed secret-key cryptography with keys longer than 40 bits. For that reason, SSL/TLS has an exportable version with weak (40-bit) keys and a domestic (North American) version with strong (128-bit) keys. Within the last several years, however, use of strong SKC has been approved for the worldwide financial community. SGC is an extension to SSL that allows financial institutions using Windows NT servers to employ strong cryptography. Both the client and server must implement SGC and the bank must have a valid SGC certificate. During the initial handshake, the server will indicate support of SGC and supply its SGC certificate; if the client wishes to use SGC and validates the server's SGC certificate, the session can employ 128-bit RC2, 128-bit RC4, 56-bit DES, or 168-bit 3DES. Microsoft supports SGC in the Windows 95/98/NT versions of Internet Explorer 4.0, Internet Information Server (IIS) 4.0, and Money 98.
   As mentioned above, SSL was designed to provide application-independent transaction security for the Internet. Although the discussion above has focused on HTTP over SSL (https/TCP port 443), SSL is also applicable to:
   

   Protocol		TCP Port Name/Number
   File Transfer Protocol (FTP)		ftps-data/989 & ftps/990
   Internet Message Access Protocol v4 (IMAP4)		imaps/993
   Lightweight Directory Access Protocol (LDAP)		ldaps/636
   Network News Transport Protocol (NNTP)		nntps/563
   Post Office Protocol v3 (POP3)		pop3s/995
   Telnet		telnets/992

   TLS was originally designed to operate over TCP. The IETF developed the Datagram Transport Layer Security (DTLS) protocol, based upon TLS, to operate over UDP. DTLS v1.2 is described in RFC 6347. (DTLS v1.0 can be found in RFC 4347.) RFC 6655 describes a suite of AES in Counter with Cipher Block Chaining - Message Authentication Code (CBC-MAC) Mode (CCM) ciphers for use with TLS and DTLS.
   

   5.8. Elliptic Curve Cryptography (ECC)

   In general, public-key cryptography systems use hard-to-solve problems as the basis of the algorithm. The most predominant algorithm today for public-key cryptography is RSA, based on the prime factors of very large integers. While RSA can be successfully attacked, the mathematics of the algorithm have not been comprised, per se; instead, computational brute-force has broken the keys. The defense is "simple" — keep the size of the integer to be factored ahead of the computational curve!
   In 1985, Elliptic Curve Cryptography (ECC) was proposed independently by cryptographers Victor Miller (IBM) and Neal Koblitz (University of Washington). ECC is based on the difficulty of solving the Elliptic Curve Discrete Logarithm Problem (ECDLP). Like the prime factorization problem, ECDLP is another "hard" problem that is deceptively simple to state: Given two points, P and Q, on an elliptic curve, find the integer n, if it exists, such that P = nQ.
   Elliptic curves combine number theory and algebraic geometry. These curves can be defined over any field of numbers (i.e., real, integer, complex) although we generally see them used over finite fields for applications in cryptography. An elliptic curve consists of the set of real numbers (x,y) that satisfies the equation:
   
   y² = x³ + ax + b
   The set of all of the solutions to the equation forms the elliptic curve. Changing a and b changes the shape of the curve, and small changes in these parameters can result in major changes in the set of (x,y) solutions.
   
   

   FIGURE 17: Elliptic curve addition.

   
   Figure 17 shows the addition of two points on an elliptic curve. Elliptic curves have the interesting property that adding two points on the elliptic curve yields a third point on the curve. Therefore, adding two points, P and Q, gets us to point R, also on the curve. Small changes in P or Q can cause a large change in the position of R.
   So let's go back to the original problem statement from above. The point Q is calculated as a multiple of the starting point, P, or, Q = nP. An attacker might know P and Q but finding the integer, n, is a difficult problem to solve. Q (i.e., nP) is the public key and n is the private key.
   ECC may be employed with many Internet standards, including CCITT X.509 certificates and certificate revocation lists (CRLs), Internet Key Exchange (IKE), Transport Layer Security (TLS), XML signatures, and applications or protocols based on the cryptographic message syntax (CMS). RFC 5639 proposes a set of elliptic curve domain parameters over finite prime fields for use in these cryptographic applications and RFC 6637 proposes additional elliptic curves for use with OpenPGP.
   RSA had been the mainstay of PKC for over a quarter-century. ECC, however, is emerging as a replacement in some environments because it provides similar levels of security compared to RSA but with significantly reduced key sizes. NIST use the following table to demonstrate the key size relationship between ECC and RSA, and the appropriate choice of AES key size:
   

   TABLE 4. ECC and RSA Key Comparison.

   ECC Key Size	RSA Key Size	Key-Size Ratio	AES Key Size
   163	1,024	1:6	n/a
   256	3,072	1:12	128
   384	7,680	1:20	192
   512	15,360	1:30	256
   Key sizes in bits.		Source: Certicom, NIST

   
   Since the ECC key sizes are so much shorter than comparable RSA keys, the length of the public key and private key is much shorter in elliptic curve cryptosystems. This results into faster processing times, and lower demands on memory and bandwidth; some studies have found that ECC is faster than RSA for signing and decryption, but slower for signature verification and encryption.
   ECC is particularly useful in applications where memory, bandwidth, and/or computational power is limited (e.g., a smartcard) and it is in this area that ECC use is expected to grow. A major champion of ECC today is Certicom; readers are urged to see their ECC tutorial.
   

   5.9. The Advanced Encryption Standard (AES) and Rijndael

   The search for a replacement to DES started in January 1997 when NIST announced that it was looking for an Advanced Encryption Standard. In September of that year, they put out a formal Call for Algorithms and in August 1998 announced that 15 candidate algorithms were being considered (Round 1). In April 1999, NIST announced that the 15 had been whittled down to five finalists (Round 2): MARS (multiplication, addition, rotation and substitution) from IBM; Ronald Rivest's RC6; Rijndael from a Belgian team; Serpent, developed jointly by a team from England, Israel, and Norway; and Twofish, developed by Bruce Schneier. In October 2000, NIST announced their selection: Rijndael.
   The remarkable thing about this entire process has been the openness as well as the international nature of the "competition." NIST maintained an excellent Web site devoted to keeping the public fully informed, at http://csrc.nist.gov/archive/aes/, which is now available as an archive site. Their Overview of the AES Development Effort has full details of the process, algorithms, and comments so I will not repeat everything here.
   In October 2000, NIST released the Report on the Development of the Advanced Encryption Standard (AES) that compared the five Round 2 algorithms in a number of categories. The table below summarizes the relative scores of the five schemes (1=low, 3=high):
   

   	Algorithm
   Category	MARS	RC6	Rijndael	Serpent	Twofish
   General security	3	2	2	3	3
   Implementation of security	1	1	3	3	2
   Software performance	2	2	3	1	1
   Smart card performance	1	1	3	3	2
   Hardware performance	1	2	3	3	2
   Design features	2	1	2	1	3

   With the report came the recommendation that Rijndael be named the AES. In February 2001, NIST released the Draft Federal Information Processing Standard (FIPS) AES Specification for public review and comment. AES contains a subset of Rijndael's capabilities (e.g., AES only supports a 128-bit block size) and uses some slightly different nomenclature and terminology, but to understand one is to understand both. The 90-day comment period ended on May 29, 2001 and the U.S. Department of Commerce officially adopted AES in December 2001, published as FIPS PUB 197.
   AES (Rijndael) Overview
   Rijndael (pronounced as in "rain doll" or "rhine dahl") is a block cipher designed by Joan Daemen and Vincent Rijmen, both cryptographers in Belgium. Rijndael can operate over a variable-length block using variable-length keys; the version 2 specification submitted to NIST describes use of a 128-, 192-, or 256-bit key to encrypt data blocks that are 128, 192, or 256 bits long; note that all nine combinations of key length and block length are possible. The algorithm is written in such a way that block length and/or key length can easily be extended in multiples of 32 bits and it is specifically designed for efficient implementation in hardware or software on a range of processors. The design of Rijndael was strongly influenced by the block cipher called Square, also designed by Daemen and Rijmen.
   Rijndael is an iterated block cipher, meaning that the initial input block and cipher key undergoes multiple rounds of transformation before producing the output. Each intermediate cipher result is called a State.
   For ease of description, the block and cipher key are often represented as an array of columns where each array has 4 rows and each column represents a single byte (8 bits). The number of columns in an array representing the state or cipher key, then, can be calculated as the block or key length divided by 32 (32 bits = 4 bytes). An array representing a State will have Nb columns, where Nb values of 4, 6, and 8 correspond to a 128-, 192-, and 256-bit block, respectively. Similarly, an array representing a Cipher Key will have Nk columns, where Nk values of 4, 6, and 8 correspond to a 128-, 192-, and 256-bit key, respectively. An example of a 128-bit State (Nb=4) and 192-bit Cipher Key (Nk=6) is shown below:
   

   s0,0 s0,1 s0,2 s0,3 s1,0 s1,1 s1,2 s1,3 s2,0 s2,1 s2,2 s2,3 s3,0 s3,1 s3,2 s3,3

   k0,0 k0,1 k0,2 k0,3 k0,4 k0,5 k1,0 k1,1 k1,2 k1,3 k1,4 k1,5 k2,0 k2,1 k2,2 k2,3 k2,4 k2,5 k3,0 k3,1 k3,2 k3,3 k3,4 k3,5

   The number of transformation rounds (Nr) in Rijndael is a function of the block length and key length, and is given by the table below:
   

   No. of Rounds Nr		Block Size
   		128 bits Nb = 4	192 bits Nb = 6	256 bits Nb = 8
   Key Size	128 bits Nk = 4	10	12	14
   	192 bits Nk = 6	12	12	14
   	256 bits Nk = 8	14	14	14

   Now, having said all of this, the AES version of Rijndael does not support all nine combinations of block and key lengths, but only the subset using a 128-bit block size. NIST calls these supported variants AES-128, AES-192, and AES-256 where the number refers to the key size. The Nb, Nk, and Nr values supported in AES are:
   

   	Parameters
   Variant	Nb	Nk	Nr
   AES-128	4	4	10
   AES-192	4	6	12
   AES-256	4	8	14

   The AES/Rijndael cipher itself has three operational stages:
   
   • AddRound Key transformation
   • Nr-1 Rounds comprising:
   • SubBytes transformation
   • ShiftRows transformation
   • MixColumns transformation
   • AddRoundKey transformation
   • A final Round comprising:
   • SubBytes transformation
   • ShiftRows transformation
   • AddRoundKey transformation
   The paragraphs below will describe the operations mentioned above. The nomenclature used below is taken from the AES specification although references to the Rijndael specification are made for completeness. The arrays s and s' refer to the State before and after a transformation, respectively (NOTE: The Rijndael specification uses the array nomenclature a and b to refer to the before and after States, respectively). The subscripts i and j are used to indicate byte locations within the State (or Cipher Key) array.
   The SubBytes transformation
   
   The substitute bytes (called ByteSub in Rijndael) transformation operates on each of the State bytes independently and changes the byte value. An S-box, or substitution table, controls the transformation. The characteristics of the S-box transformation as well as a compliant S-box table are provided in the AES specification; as an example, an input State byte value of 107 (0x6b) will be replaced with a 127 (0x7f) in the output State and an input value of 8 (0x08) would be replaced with a 48 (0x30).
   One way to think of the SubBytes transformation is that a given byte in State s is given a new value in State s' according to the S-box. The S-box, then, is a function on a byte in State s so that:
   
   s'_i,j = S-box (s_i,j)
   The more general depiction of this transformation is shown by:
   

   s0,0 s0,1 s0,2 s0,3 s1,0 s1,1 s1,2 s1,3 s2,0 s2,1 s2,2 s2,3 s3,0 s3,1 s3,2 s3,3

   ====>

   S-box

   ====>

   s'0,0 s'0,1 s'0,2 s'0,3 s'1,0 s'1,1 s'1,2 s'1,3 s'2,0 s'2,1 s'2,2 s'2,3 s'3,0 s'3,1 s'3,2 s'3,3

   The ShiftRows transformation
   The shift rows (called ShiftRow in Rijndael) transformation cyclically shifts the bytes in the bottom three rows of the State array. According to the more general Rijndael specification, rows 2, 3, and 4 are cyclically left-shifted by C1, C2, and C3 bytes, respectively, per the table below:
   

   Nb	C1	C2	C3
   4	1	2	3
   6	1	2	3
   8	1	3	4

   The current version of AES, of course, only allows a block size of 128 bits (Nb = 4) so that C1=1, C2=2, and C3=3. The diagram below shows the effect of the ShiftRows transformation on State s:
   

   State s s0,0 s0,1 s0,2 s0,3 s1,0 s1,1 s1,2 s1,3 s2,0 s2,1 s2,2 s2,3 s3,0 s3,1 s3,2 s3,3

   ----------- no shift ----------->  ----> left-shift by C1 (1) ---->  ----> left-shift by C2 (2) ---->  ----> left-shift by C3 (3) ---->

   State s' s0,0 s0,1 s0,2 s0,3 s1,1 s1,2 s1,3 s1,0 s2,2 s2,3 s2,0 s2,1 s3,3 s3,0 s3,1 s3,2

   The MixColumns transformation
   The mix columns (called MixColumn in Rijndael) transformation uses a mathematical function to transform the values of a given column within a State, acting on the four values at one time as if they represented a four-term polynomial. In essence, if you think of MixColumns as a function, this could be written:
   
   s'_i,c = MixColumns (s_i,c)
   for 0<=i<=3 for some column, c. The column position doesn't change, merely the values within the column.
   Round Key generation and the AddRoundKey transformation
   The AES Cipher Key can be 128, 192, or 256 bits in length. The Cipher Key is used to derive a different key to be applied to the block during each round of the encryption operation. These keys are called the Round Keys and each will be the same length as the block, i.e., Nb 32-bit words (words will be denoted W).
   The AES specification defines a key schedule by which the original Cipher Key (of length Nk 32-bit words) is used to form an Expanded Key. The Expanded Key size is equal to the block size times the number of encryption rounds plus 1, which will provide Nr+1 different keys. (Note that there are Nr encipherment rounds but Nr+1 AddRoundKey transformations.)
   Consider that AES uses a 128-bit block and either 10, 12, or 14 iterative rounds depending upon key length. With a 128-bit key, for example, we would need 1408 bits of key material (128x11=1408), or an Expanded Key size of 44 32-bit words (44x32=1408). Similarly, a 192-bit key would require 1664 bits of key material (128x13), or 52 32-bit words, while a 256-bit key would require 1920 bits of key material (128x15), or 60 32-bit words. The key expansion mechanism, then, starts with the 128-, 192-, or 256-bit Cipher Key and produces a 1408-, 1664-, or 1920-bit Expanded Key, respectively. The original Cipher Key occupies the first portion of the Expanded Key and is used to produce the remaining new key material.
   The result is an Expanded Key that can be thought of and used as 11, 13, or 15 separate keys, each used for one AddRoundKey operation. These, then, are the Round Keys. The diagram below shows an example using a 192-bit Cipher Key (Nk=6), shown in magenta italics:
   

   Expanded Key:	W0	W1	W2	W3	W4	W5	W6	W7	W8	W9	W10	W11	W12	W13	W14	W15	...	W44	W45	W46	W47	W48	W49	W50	W51
   Round keys:	Round key 0				Round key 1				Round key 2				Round key 3				...	Round key 11				Round key 12

   The AddRoundKey (called Round Key addition in Rijndael) transformation merely applies each Round Key, in turn, to the State by a simple bit-wise exclusive OR operation. Recall that each Round Key is the same length as the block.
   Summary
   Ok, I hope that you've enjoyed reading this as much as I've enjoyed writing it — and now let me guide you out of the microdetail! Recall from the beginning of the AES overview that the cipher itself comprises a number of rounds of just a few functions:
   
   • SubBytes takes the value of a word within a State and substitutes it with another value by a predefined S-box
   • ShiftRows circularly shifts each row in the State by some number of predefined bytes
   • MixColumns takes the value of a 4-word column within the State and changes the four values using a predefined mathematical function
   • AddRoundKey XORs a key that is the same length as the block, using an Expanded Key derived from the original Cipher Key
   
   

   Cipher (byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)]) begin byte state[4,Nb] state = in AddRoundKey(state, w) for round = 1 step 1 to Nr-1 SubBytes(state) ShiftRows(state) MixColumns(state) AddRoundKey(state, w+round*Nb) end for SubBytes(state) ShiftRows(state) AddRoundKey(state, w+Nr*Nb) out = state end FIGURE 18: AES pseudocode.

   
   As a last and final demonstration of the operation of AES, Figure 18 is a pseudocode listing for the operation of the AES cipher. In the code:
   
   • in[] and out[] are 16-byte arrays with the plaintext and cipher text, respectively. (According to the specification, both of these arrays are actually 4*Nb bytes in length but Nb=4 in AES.)
   • state[] is a 2-dimensional array containing bytes in 4 rows and 4 columns. (According to the specification, this arrays is 4 rows by Nb columns.)
   • w[] is an array containing the key material and is 4*(Nr+1) words in length. (Again, according to the specification, the multiplier is actually Nb.)
   • AddRoundKey(), SubBytes(), ShiftRows(), and MixColumns() are functions representing the individual transformations.

   5.10. Cisco's Stream Cipher

   Stream ciphers take advantage of the fact that:
   
   x XOR y XOR y = x
   One of the encryption schemes employed by Cisco routers to encrypt passwords is a stream cipher. It uses the following fixed keystream (thanks also to Jason Fossen for independently extending and confirming this string):
   
   dsfd;kfoA,.iyewrkldJKDHSUBsgvca69834ncx
   When a password is to be encrypted, the password function chooses a number between 0 and 15, and that becomes the offset into the keystream. Password characters are then XORed byte-by-byte with the keystream according to:
   
   C_i = P_i XOR K_(offset+i)
   where K is the keystream, P is the plaintext password, and C is the ciphertext password.
   Consider the following example. Suppose we have the password abcdefgh. Converting the ASCII characters yields the hex string 0x6162636465666768.
   The keystream characters and hex code that supports an offset from 0 to 15 bytes and a password length up to 24 bytes is:
   
     d s f d ; k f o A , . i y e w r k l d J K D H S U B s g v c a 6 9 8 3 4 n c x
   0x647366643b6b666f412c2e69796577726b6c644a4b4448535542736776636136393833346e6378
   Let's say that the function decides upon a keystream offset of 6 bytes. We then start with byte 6 of the keystream (start counting the offset at 0) and XOR with the password:
   
       0x666f412c2e697965
   XOR 0x6162636465666768
       ------------------
       0x070D22484B0F1E0D
   The password would now be displayed in the router configuration as:
   
   password 7 06070D22484B0F1E0D
   where the "7" indicates the encryption type, the leading "06" indicates the offset into the keystream, and the remaining bytes are the encrypted password characters.
   (Decryption is pretty trivial so that exercise is left to the reader. If you need some help with byte-wise XORing, see http://www.garykessler.net/library/byte_logic_table.html. If you'd like some programs that do this, see http://www.garykessler.net/software/cisco7.zip.)
   

   5.11. TrueCrypt

   TrueCrypt is an open source, on-the-fly crypto system that can be used on devices supports by Linux, MacOS, and Windows. First released in 2004, TrueCrypt can be employed to encrypt a partition on a disk or an entire disk.
   TrueCrypt uses a variety of encryption schemes, including AES, Serpent, and Twofish. A TrueCrypt volume is stored as a file that appears to be filled with random data, thus has no specific file signature. (It is true that a TrueCrypt container will pass a chi-square (Χ²) randomness test, but that is merely a general indicator of possibly encrypted content. An additional clue is that a TrueCrypt container will also appear on a disk as a file that is some increment of 512 bytes in size. While these indicators might raise a red flag, they don't rise to the level of clearly indentifying a TrueCrypt volume.)
   When a user creates a TrueCrypt volume, a number of parameters need to be defined, such as the size of the volume and the password. To access the volume, the TrueCrypt program is employed to find the TrueCrypt encrypted file, which is then mounted as a new drive on the host system.
   
   

   FIGURE 19: TrueCrypt screen shot (Windows).

   
   
   

   FIGURE 20: TrueCrypt screen shot (MacOS).

   
   Consider this example where an encrypted TrueCrypt volume is stored as a file named James on a thumb drive. On a Windows system, this thumb drive has been mounted as device E:. If one were to view the E: device, any number of files might be found. The TrueCrypt application is used to mount the TrueCrypt file; in this case, the user has chosen to mount the TrueCrypt volume as device K: (Figure 19). Alternatively, the thumb drive could be used with a Mac system, where it has been mounted as the /Volumes/JIMMY volume. TrueCrypt mounts the encrypted file, James, and it is now accessible to the system (Figure 20).
   
   

   FIGURE 21: TrueCrypt hidden encrypted volume within an encrypted volume (from http://www.truecrypt.org/images/docs/hidden-volume.gif).

   
   One of the most interesting — certainly one of the most controversial — features of TrueCrypt is called plausible deniability, protection in case a user is "compelled" to turn over the encrypted volume's password. When the user creates a TrueCrypt volume, he/she chooses whether to create a standard or hidden volume. A standard volume has a single password, while a hidden volume is created within a standard volume and uses a second password. As shown in Figure 21, the unallocated (free) space in a TrueCrypt volume is always filled with random data, thus it is impossible to differentiate a hidden encrypted volume from a standard volume's free space.
   To access the hidden volume, the file is mounted as shown above and the user enters the hidden volume's password. When under duress, the user would merely enter the password of the standard (i.e., non-hidden) TrueCrypt volume.
   Complete information about TrueCrypt can be found at the TrueCrypt Web Site or in the TrueCrypt Tutorial.
   

   An active area of research in the digital forensics community is to find methods with which to detect hidden TrueCrypt volumes. Most of the methods do not detect the presence of a hidden volume, per se, but infer the presence by forensic remnants left over. As an example, both Mac and Windows system usually have a file or registry entry somewhere containing a cached list of the names of mounted volumes. This list would, naturally, include the name of TrueCrypt volumes, both standard and hidden. If the user gives a name to the hidden volume, it would appear in such a list. If an investigator were somehow able to determine that there were two TrueCrypt volume names but only one TrueCrypt device, the inference would be that there was a hidden volume. A good summary paper that also describes ways to infer the presence of hidden volumes — at least on some Windows systems — can be found in "Detecting Hidden Encrypted Volumes" (Hargreaves & Chivers).

   5.12. Encrypting File System (EFS)

   Microsoft introduced the Encrypting File System (EFS) into the NTFS v3.0 file system. EFS can be used to encrypt individual files, directories, or entire volumes. While off by default, EFS encryption can be easily enabled via Windows Explorer by right-clicking on the file, directory, or volume to be encrypted, selecting Properties, Advanced, and Encrypt contents to secure data (Figure 22). Note that encrypted files and directories are displayed in green in Windows Explorer.
   
   

   FIGURE 22: EFS and Windows Explorer.

   
   The Windows command prompt provides an easy tool with which to detect EFS-encrypted files on a disk. The cipher command has a number of options, but the /u/n switches can be used to list all encrypted files on a drive (Figure 23).
   
   

   FIGURE 23: The cipher command.

   
   EFS supports a variety of secret key encryption schemes, including DES, DESX, and AES, as well as RSA public-key encryption. The operation of EFS — at least at the theoretical level — is clever and simple.
   When a file is saved to disk:
   
   • A random File Encryption Key (FEK) is generated by the operating system.
   • The file contents are encrypted using one of the SKC schemes and the FEK.
   • The FEK is stored with the file, encrypted with the user's RSA public key. In addition, the FEK is encrypted with the RSA public key of any other authorized users and, optionally, a recovery agent's RSA public key.
   When the file is opened:
   
   • The FEK is recovered using the RSA private key of the user, another authorized user, or the recovery agent.
   • The FEK is used to decrypt the file's contents.
   There are weaknesses with the system, most of which are related to key management. As an example, the RSA private key can be stored on an external device such as a floppy disk (yes, really!), thumb drive, or smart card. In practice, however, this is rarely done; the user's private RSA key is on the hard drive. In addition, early EFS implementations (prior to Windows XP SP2) tied the key to the username; later implementations employ the user's password.
   A more serious implementation issue is that a backup file named esf0.tmp is created prior to a file being encrypted. After the encryption operation, the backup file is deleted — not wiped — leaving an unencrypted version of the file available to be undeleted. For this reason, it is best to use encrypted directories because the temporary backup file is protected by being in an encrypted directory.
   
   

   FIGURE 24: EFS key storage. (Source: NTFS.com)

   
   The EFS information is stored as a named stream in the $LOGGED_UTILITY_STREAM Attribute (attribute type 256 [0x100]). This information includes (Figure 24):
   
   • A Data Decryption Field (DDF) for every user authorized to decrypt the file, containing the user's Security Identifier (SID), the FEK encrypted with the user's RSA public key, and other information.
   • A Data Recovery Field (DRF) with the encrypted FEK for every method of data recovery
   Files in an NTFS file system maintain a number of attributes which contain the system metadata (e.g., the $STANDARD_INFORMATION attribute maintains the file timestamps and the $FILE_NAME attribute contains the file name). Files encrypted with EFS store the keys, as stated above, in a data stream named $EFS within the $LOGGED_UTILITY_STREAM attribute. Figure 25 shows the partial contents of the Master File Table (MFT) attributes for an EFS encrypted file.
   
   

   Master File Table (MFT) Parser V1.4 - Gary C. Kessler (7 June 2012) : : 0056-0059 Attribute type: 0x10-00-00-00 [$STANDARD_INFORMATION] 0060-0063 Attribute length: 0x60-00-00-00 [96 bytes] 0064 Non-resident flag: 0x00 [Attribute is resident] : : 0152-0155 Attribute type: 0x30-00-00-00 [$FILE_NAME] 0156-0159 Attribute length: 0x78-00-00-00 [120 bytes] 0160 Non-resident flag: 0x00 [Attribute is resident] : : 0392-0395 Attribute type: 0x40-00-00-00 [$VOLUME_VERSION/$OBJECT_ID] 0396-0399 Attribute length: 0x28-00-00-00 [40 bytes] 0400 Non-resident flag: 0x00 [Attribute is resident] : : 0432-0435 Attribute type: 0x80-00-00-00 [$DATA] 0436-0439 Attribute length: 0x48-00-00-00 [72 bytes] 0440 Non-resident flag: 0x01 [Attribute is non-resident] : : 0504-0507 Attribute type: 0x00-01-00-00 [$LOGGED_UTILITY_STREAM] 0508-0511 Attribute length: 0x50-00-2E-00 [80 bytes (ignore two high-order bytes)] 0512 Non-resident flag: 0x01 [Attribute is non-resident] : 0568-0575 Name: 0x24-00-45-00-46-00-53-00 [$EFS] FIGURE 25: The $LOGGED_UTILITY_STREAM Attribute.